
| A. | 0>m1>m2 | B. | 0>m2>m1 | C. | m2>m1>0 | D. | m1>m2>0 |
分析 设f(x)=m1x2+$\frac{1}{3}$x+1,方程f(x)=0的两实根为x1,x2(x1<x2),x3,x4是一元二次方程m2x2+$\frac{1}{3}$x+1=0的两根,所以由x1<x3<x4<x2成立,即x3,x4在两实根x1,x2之间,可由根的分布的相关知识将这一关系转化为不等式,得出m1与m2的关系.
解答 解:∵x1,x2是一元二次方程m1x2+$\frac{1}{3}$x+1=0的两根,
∴m1x12+$\frac{1}{3}$x1+1=0,m1x22+$\frac{1}{3}$x2+1=0,
∴f(x3)=m1x32+$\frac{1}{3}$x3+1,f(x4)=m1x42+$\frac{1}{3}$x4+1,
∵x3,x4是一元二次方程m2x2+$\frac{1}{3}$x+1=0的两根,
∴m2x32+$\frac{1}{3}$x3+1=0,m2x42+$\frac{1}{3}$x4+1=0,
∴f(x3)=(m1-m2)x32,f(x4)=(m1-m2)x42,
∵x1<x3<x4<x2<0,
∴$\left\{\begin{array}{l}{{m}_{1}>0}\\{{m}_{2}>0}\\{f({x}_{3})<0}\\{f({x}_{4})<0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{m}_{1}>0}\\{{m}_{2}>0}\\{{m}_{1}-{m}_{2}<0}\end{array}\right.$,
∴m2>m1>0.
故选:C.
点评 本题考查一元二次方程的根的分布与系数的关系,解答的关键是对二次函数图象的特征的把握,是一道关于二次函数的综合性很强的题目.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:填空题
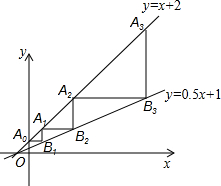 如图,直线y=x+2与y轴相交于点A0,过点A0作x轴的平行线交直线y=0.5x+1于点B1,过点B1作y轴的平行线交直线y=x+2于点A1,再过点A1作x轴的平行线交直线y=0.5x+1于点B2,过点B2作y轴的平行线交直线y=x+2于点A2,…,依此类推,得到直线y=x+2上的点A1,A2,A3,…,与直线y=0.5x+1上的点B1,B2,B3,…,则An-1Bn的长为2n.
如图,直线y=x+2与y轴相交于点A0,过点A0作x轴的平行线交直线y=0.5x+1于点B1,过点B1作y轴的平行线交直线y=x+2于点A1,再过点A1作x轴的平行线交直线y=0.5x+1于点B2,过点B2作y轴的平行线交直线y=x+2于点A2,…,依此类推,得到直线y=x+2上的点A1,A2,A3,…,与直线y=0.5x+1上的点B1,B2,B3,…,则An-1Bn的长为2n.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一个正方体,六个面分别写着六个连续的整数,且每个相对面上的两个数之和相等,如图所示,你能看到的数为7,10,11,则六个整数的和为( )
一个正方体,六个面分别写着六个连续的整数,且每个相对面上的两个数之和相等,如图所示,你能看到的数为7,10,11,则六个整数的和为( )| A. | 51 | B. | 57 | C. | 58 | D. | 52 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 | 从未听说 |
| 频数 | 40 | 60 | 48 | 36 | 16 |
| 频率 | 0.2 | m | 0.24 | 0.18 | 0.08 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com