
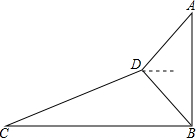
 如图,小明为了测量大楼AB的高度,他从点C出发,沿着斜坡面CD走104米到点D处,测得大楼顶部点A的仰角为37°,大楼底部点B的俯角为45°,已知斜坡CD的坡度为i=1:2.4.(参考书据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,小明为了测量大楼AB的高度,他从点C出发,沿着斜坡面CD走104米到点D处,测得大楼顶部点A的仰角为37°,大楼底部点B的俯角为45°,已知斜坡CD的坡度为i=1:2.4.(参考书据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)分析 (1)作DE⊥AB于E,作DF⊥BC于F,y由CD的坡度为i=1:2.4,CD=104米,得到$\frac{DF}{CF}$=1:2.4,根据勾股定理列方程,即可得到结论;
(2)根据矩形的性质得到BE=40m,由等腰直角三角形的性质得到DE=BE=40m,根据三角函数的定义即可得到结果.
解答 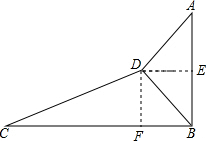 解:(1)作DE⊥AB于E,作DF⊥BC于F,
解:(1)作DE⊥AB于E,作DF⊥BC于F,
∵CD的坡度为i=1:2.4,CD=104米,
∴$\frac{DF}{CF}$=1:2.4,
∴$\sqrt{D{F}^{2}+(2.4DF)^{2}}$=104,
∴DF=40(米);
(2)∵DF=40m,
∴BE=40m,
∵∠BDE=45°,
∴DE=BE=40m,
在Rt△ADE中,∠ADE=37°,
∴AE=tan37°•40=30(米)
∴AB=AE+BE=70m.
点评 本题考查了仰角与俯角的知识.此题难度适中,注意能借助仰角与俯角构造直角三角形并解直角三角形是解此题的关键,注意掌握数形结合思想与方程思想的应用.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
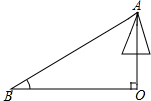 如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为30tanα米(用三角函数表示)
如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为30tanα米(用三角函数表示)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1±$\sqrt{6}$ | B. | $\sqrt{6}$-1 | C. | 1-$\sqrt{6}$ | D. | 1+$\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3×108 | B. | 3×107 | C. | 3×106 | D. | 0.3×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
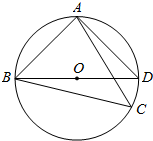 如图,点C为△ABD的外接圆上的一动点(点C不在$\widehat{BAD}$上,且不与点B,D重合),∠ACB=∠ABD=45°
如图,点C为△ABD的外接圆上的一动点(点C不在$\widehat{BAD}$上,且不与点B,D重合),∠ACB=∠ABD=45°查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com