
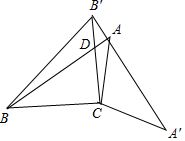
 △ABC中,∠ABC=30°,AC=$\sqrt{7}$,BC=2$\sqrt{3}$,将△ABC绕着点C顺时针旋转,A、B两点的对应点分别为A′,B′,若A′,B′刚好经过点A,AB,B′C交于点D,则$\frac{AD}{DB}$=$\frac{7}{48}$.
△ABC中,∠ABC=30°,AC=$\sqrt{7}$,BC=2$\sqrt{3}$,将△ABC绕着点C顺时针旋转,A、B两点的对应点分别为A′,B′,若A′,B′刚好经过点A,AB,B′C交于点D,则$\frac{AD}{DB}$=$\frac{7}{48}$. 分析 作辅助线,构建直角三角形,根据30°角所对的直角边是斜边的一半依次求出CG、BG、AH、A′H的长,再由勾股定理列方程求AG的长,证明△CDG∽△ADM,得$\frac{CG}{AM}=\frac{CD}{AD}$,则CD=2$\sqrt{3}$AD,设AD=x,则CD=2$\sqrt{3}$x,GD=2-x,根据勾股定理列方程求出x的值,从而得出AD和BD的长,相比即可.
解答  解:过C作CG⊥AB于G,CH⊥AA′于H,过A作AM⊥B′C于M,
解:过C作CG⊥AB于G,CH⊥AA′于H,过A作AM⊥B′C于M,
在Rt△BGC中,∠ABC=30°,BC=2$\sqrt{3}$,
∴CG=$\frac{1}{2}$BC=$\frac{1}{2}$×$2\sqrt{3}$=$\sqrt{3}$,
BG=$\sqrt{B{C}^{2}-C{G}^{2}}$=$\sqrt{(2\sqrt{3})^{2}-(\sqrt{3})^{2}}$=3,
同理得:AG=2,
由旋转得:∠BAC=∠B′A′C,AC=A′C,
∴∠CAA′=∠B′A′C,
∴∠BAC=∠CAA′,
∴CG=CH=$\sqrt{3}$,
由勾股定理得:AH=$\sqrt{(\sqrt{7})^{2}-(\sqrt{3})^{2}}$=2,
∵AC=A′C,CH⊥AA′,
∴AH=A′H=2,
∵A′B′=AB=2+3=5,
∴AB′=A′B′-AA′=5-4=1,
Rt△AMB′中,∠CB′A′=30°,
∴AM=$\frac{1}{2}$AB′=$\frac{1}{2}$,
∵∠CGD=∠DMA=90°,
∠CDG=∠ADM,
∴△CDG∽△ADM,
∴$\frac{CG}{AM}=\frac{CD}{AD}$,
∴$\frac{\sqrt{3}}{\frac{1}{2}}$=$\frac{CD}{AD}$=$\frac{2\sqrt{3}}{1}$,
∴CD=2$\sqrt{3}$AD,
设AD=x,则CD=2$\sqrt{3}$x,GD=2-x,
由勾股定理得:CD2=DG2+CG2,
$(2\sqrt{3}x)^{2}$=$(2-x)^{2}+(\sqrt{3})^{2}$,
(x+1)(11x-7)=0,
x1=-1(舍),x2=$\frac{7}{11}$,
∴AD=$\frac{7}{11}$,
∴BD=5-$\frac{7}{11}$=$\frac{48}{11}$,
∴$\frac{AD}{BD}$=$\frac{\frac{7}{11}}{\frac{48}{11}}$=$\frac{7}{48}$,
故答案为:$\frac{7}{48}$.
点评 本题考查了旋转的性质,明确旋转前后的对应边相等,对应角相等,以30°为条件,构建直角三角形,则利用一边的长,求其它两边,并与方程相结合,利用勾股定理列方程得出结论.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
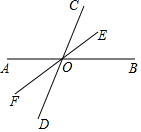 如图,直线AB、CD相交于点O,OE是∠BOC的平分线,OF是OE的反向延长线.
如图,直线AB、CD相交于点O,OE是∠BOC的平分线,OF是OE的反向延长线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com