
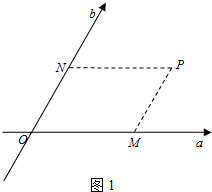
 如图1,在平面内取一点O,过点O作两条夹角为60°的数轴,使它们以点O为公共原点且具有相同的单位长度,这样在平面内建立的坐标系称为斜坐标系,我们把水平放置的数轴称为横轴(记作a轴),将斜向放置的数轴称为斜轴(记作b轴).类似
如图1,在平面内取一点O,过点O作两条夹角为60°的数轴,使它们以点O为公共原点且具有相同的单位长度,这样在平面内建立的坐标系称为斜坐标系,我们把水平放置的数轴称为横轴(记作a轴),将斜向放置的数轴称为斜轴(记作b轴).类似

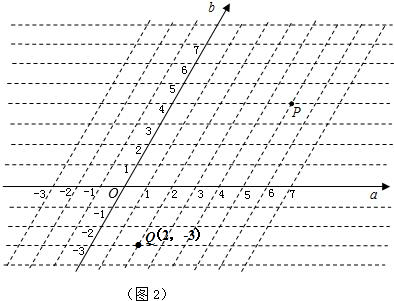 解:(1)点P(5,4),点Q坐标如图所示;(4分)
解:(1)点P(5,4),点Q坐标如图所示;(4分)
|


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
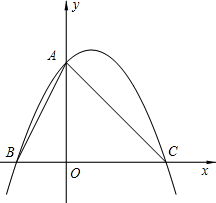 ,点C、A分别在x、y轴的正半轴上,一条抛物线经过点A、C及点B(-3,0).
,点C、A分别在x、y轴的正半轴上,一条抛物线经过点A、C及点B(-3,0).查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•吉林)如图,沿AC方向开山修一条公路,为了加快施工速度,要在小山的另一边寻找点E同时施工.从AC上的一点B取∠ABD=127°,沿BD的方向前进,取∠BDE=37°,测得BD=520m,并且AC,BD和DE在同一平面内.
(2012•吉林)如图,沿AC方向开山修一条公路,为了加快施工速度,要在小山的另一边寻找点E同时施工.从AC上的一点B取∠ABD=127°,沿BD的方向前进,取∠BDE=37°,测得BD=520m,并且AC,BD和DE在同一平面内.查看答案和解析>>
科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com