
ЁОЬтФПЁПЬхг§ЖЭСЖЖдбЇЩњЕФНЁПЕГЩГЄгазХЩюдЖЕФгАЯьЃЎФГжабЇ ПЊеЙСЫЫФЯюЧђРрЛюЖЏЃКAЃКЦЙХвЧђЃЛBЃКзуЧђЃЛCЃКХХЧђЃЛDЃКРКЧђЃЎЭѕРЯЪІЖдбЇЩњзюЯВЛЖЕФвЛЯюЧђРрЛюЖЏНјааСЫГщбљЕїВщЃЈУПШЫжЛЯовЛЯюЃЉЃЌВЂНЋЕїВщНсЙћЛцжЦГЩЭМ 1ЃЌЭМ2СНЗљВЛЭъећЕФЭГМЦЭМЃЎ
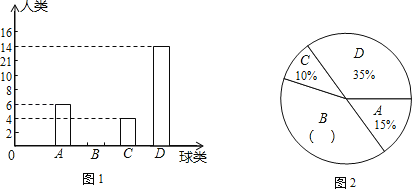
ЧыИљОнЭМжааХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉВЮМгДЫДЮЕїВщЕФбЇЩњзмЪ§ЪЧЁЁ ЁЁШЫЃЛНЋЭМ1ЁЂЭМ2ЕФЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉвбжЊдкБЛЕїВщЕФзюЯВЛЖХХЧђЯюФПЕФ4УћбЇЩњжажЛга1УћХЎЩњЃЌЯжДгет4УћбЇЩњжаШЮвтГщШЁ2УћбЇЩњВЮМгаЃХХЧђЖгЃЌЧыгУСаБэЗЈЛђЛЪїзДЭМЕФЗНЗЈЃЌЧѓГіЧЁКУГщЕНвЛУћФаЩњКЭвЛУћХЎЩњЕФИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉ40ЃЌЯъМћНтЮіЃЛЃЈ2ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнAЛюЖЏЕФШЫЪ§МАЦфАйЗжБШПЩЕУзмШЫЪ§ЃЌгУзмШЫЪ§МѕШЅAЁЂCЁЂDЕФШЫЪ§ЧѓГіBЛюЖЏЕФШЫЪ§ЃЌгУBЯюЕФШЫЪ§Г§вдзмШЫЪ§МДПЩЧѓГіBЯюЫљеМЕФАйЗжБШЃЌДгЖјВЙШЋЭГМЦЭМЃЛ
ЃЈ2ЃЉСаБэЕУГіЫљгаЕШПЩФмНсЙћЃЌдйДгжаевЕНЧЁКУГщЕНвЛУћФаЩњвЛУћХЎЩњЕФНсЙћЪ§ЃЌМЬЖјИљОнИХТЪЙЋЪНМЦЫуПЩЕУЃЎ
НтЃКЃЈ1ЃЉБОДЮЕїВщЕФбЇЩњзмШЫЪ§ЮЊ6ЁТ15%ЃН40ШЫЃЌ
BЯюЛюЖЏЕФШЫЪ§ЮЊ40-(6+4+14)ЃН16ЃЌ
BЯюЫљеМЕФАйЗжБШЪЧ:![]() %=40%ЃЛ
%=40%ЃЛ
ВЙШЋЭГМЦЭМШчЯТЃК

ЙЪД№АИЮЊЃК40ЃЛ
ЃЈ2ЃЉСаБэШчЯТЃК
Фа | Фа | Фа | ХЎ | |
Фа | ЃЈФаЃЌФаЃЉ | ЃЈФаЃЌФаЃЉ | ЃЈФаЃЌХЎЃЉ | |
Фа | ЃЈФаЃЌФаЃЉ | ЃЈФаЃЌФаЃЉ | ЃЈФаЃЌХЎЃЉ | |
Фа | ЃЈФаЃЌФаЃЉ | ЃЈФаЃЌФаЃЉ | ЃЈФаЃЌХЎЃЉ | |
ХЎ | ЃЈХЎЃЌФаЃЉ | ЃЈХЎЃЌФаЃЉ | ЃЈХЎЃЌФаЃЉ |
гЩБэПЩжЊзмЙВга12жжНсЙћЃЌУПжжНсЙћГіЯжЕФПЩФмадЯрЭЌЃЌЦфжаЧЁКУГщЕНвЛУћФаЩњКЭвЛУћХЎЩњЕФНсЙћга6жжЃЌ
ЫљвдГщЕНвЛУћФаЩњКЭвЛУћХЎЩњЕФИХТЪЪЧ![]() ЃЎ
ЃЎ


 УППЮБиСЗЯЕСаД№АИ
УППЮБиСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
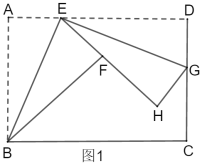
ЁОЬтФПЁПШчЭМ(1)ЃЌдкОиаЮABCDжаЃЌADЃНnABЃЌЕуMЃЌPЗжБ№дкБпABЃЌADЩЯ(ОљВЛгыЖЫЕужиКЯ)ЃЌЧвAPЃНnAMЃЌвдAPКЭAMЮЊСкБпзїОиаЮAMNPЃЌСЌНгANЃЌCN.
ЃЈЮЪЬтЗЂЯжЃЉ
ЃЈ1ЃЉШчЭМ(2)ЃЌЕБnЃН1ЪБЃЌBMгыPDЕФЪ§СПЙиЯЕЮЊ ЃЌCNгыPDЕФЪ§СПЙиЯЕЮЊ .
ЃЈРрБШЬНОПЃЉ
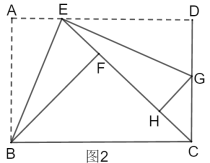
ЃЈ2ЃЉШчЭМ(3)ЃЌЕБnЃН2ЪБЃЌОиаЮAMNPШЦЕуAЫГЪБеыа§зЊЃЌСЌНгPDЃЌдђCNгыPDжЎМфЕФЪ§СПЙиЯЕЪЧЗёЗЂЩњБфЛЏЃПШєВЛБфЃЌЧыОЭЭМ(3)ИјГіжЄУїЃЛШєБфЛЏЃЌЧыаДГіЪ§СПЙиЯЕЃЌВЂОЭЭМ(3)ЫЕУїРэгЩ.
ЃЈЭиеЙбгЩьЃЉ
ЃЈ3ЃЉдк(2)ЕФЬѕМўЯТЃЌвбжЊADЃН4ЃЌAPЃН2ЃЌЕБОиаЮAMVPа§зЊжСCЃЌNЃЌMШ§ЕуЙВЯпЪБЃЌЧыжБНгаДГіЯпЖЮCNЕФГЄ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌелЕўОиаЮ![]() ЃЌОпЬхВйзїЃКЂйЕу
ЃЌОпЬхВйзїЃКЂйЕу![]() ЮЊ
ЮЊ![]() БпЩЯвЛЕуЃЈВЛгы
БпЩЯвЛЕуЃЈВЛгы![]() ЁЂ
ЁЂ![]() жиКЯЃЉЃЌАб
жиКЯЃЉЃЌАб![]() би
би![]() ЫљдкЕФжБЯпелЕўЃЌ
ЫљдкЕФжБЯпелЕўЃЌ![]() ЕуЕФЖдГЦЕуЮЊ
ЕуЕФЖдГЦЕуЮЊ![]() ЕуЃЛЂкЙ§Еу
ЕуЃЛЂкЙ§Еу![]() Ждел
Ждел![]() ЃЌелКл
ЃЌелКл![]() ЫљдкЕФжБЯпНЛ
ЫљдкЕФжБЯпНЛ![]() гкЕу
гкЕу![]() ЁЂ
ЁЂ![]() ЕуЕФЖдГЦЕуЮЊ
ЕуЕФЖдГЦЕуЮЊ![]() ЕуЃЎ
ЕуЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() Ёз
Ёз![]() ЃЎ
ЃЎ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЂйЕу![]() дквЦЖЏЕФЙ§ГЬжаЃЌЧѓ
дквЦЖЏЕФЙ§ГЬжаЃЌЧѓ![]() ЕФзюДѓжЕЃЎ
ЕФзюДѓжЕЃЎ
ЂкШчЭМ2ЃЌШєЕу![]() ЧЁдкжБЯп
ЧЁдкжБЯп![]() ЩЯЃЌСЌНг
ЩЯЃЌСЌНг![]() ЃЌЧѓЯпЖЮ
ЃЌЧѓЯпЖЮ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§![]() ЕФЭМЯѓОЙ§Еу
ЕФЭМЯѓОЙ§Еу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФжЕКЭЭМЯѓЕФЖЅЕузјБъЃЛ
ЕФжЕКЭЭМЯѓЕФЖЅЕузјБъЃЛ
ЃЈ2ЃЉЕу![]() дкИУЖўДЮКЏЪ§ЭМЯѓЩЯЃЎ
дкИУЖўДЮКЏЪ§ЭМЯѓЩЯЃЎ
ЂйЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЂкШєЕу![]() ЕН
ЕН![]() жсЕФОрРыаЁгк2ЃЌЧыИљОнЭМЯѓжБНгаДГі
жсЕФОрРыаЁгк2ЃЌЧыИљОнЭМЯѓжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЂлжБНгаДГіЕу![]() гыжБЯп
гыжБЯп![]() ЕФОрРыаЁгк
ЕФОрРыаЁгк![]() ЪБ
ЪБ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
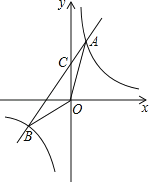
ЁОЬтФПЁПШчЭМЃЌвбжЊвЛДЮКЏЪ§y=kx+bЕФЭМЯѓгыЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓНЛгкAЃЌBСНЕуЃЌЕуAЕФКсзјБъЪЧ2ЃЌЕуBЕФзнзјБъЪЧЃ2ЃЎ
ЕФЭМЯѓНЛгкAЃЌBСНЕуЃЌЕуAЕФКсзјБъЪЧ2ЃЌЕуBЕФзнзјБъЪЧЃ2ЃЎ
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЁїAOBЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
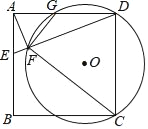
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌEЪЧABЩЯвЛЕуЃЌСЌНгDEЃЎЙ§ЕуAзїAFЁЭDEЃЌДЙзуЮЊFЃЌЁбOОЙ§ЕуCЁЂDЁЂFЃЌгыADЯрНЛгкЕуGЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїAFGЁзЁїDFCЃЛ
ЃЈ2ЃЉШєе§ЗНаЮABCDЕФБпГЄЮЊ4ЃЌAEЃН1ЃЌЧѓЁбOЕФАыОЖЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,ХзЮяЯпy=ax2+bx+c(aЁй0)ОЙ§Еу ОЙ§ЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ5ЃЌЉ6ЃЉЃЌCЃЈ6ЃЌ0ЃЉ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМЃЌдкжБЯпABЯТЗНЕФХзЮяЯпЩЯЪЧЗёДцдкЕуPЪЙЫФБпаЮPACBЕФУцЛ§зюДѓЃПШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЕуQЮЊХзЮяЯпЕФЖдГЦжсЩЯЕФвЛИіЖЏЕуЃЌЪджИГіЁїQABЮЊЕШбќШ§НЧаЮЕФЕуQвЛЙВгаМИИіЃПВЂЧыЧѓГіЦфжаФГвЛИіЕуQЕФзјБъ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЮЊВтСПКгАЖСНЕЦЫў![]() ЃЌ
ЃЌ![]() жЎМфЕФОрРыЃЌаЁУїдкКгЖдАЖ
жЎМфЕФОрРыЃЌаЁУїдкКгЖдАЖ![]() ДІВтЕУЕЦЫў
ДІВтЕУЕЦЫў![]() дкББЦЋЖЋ
дкББЦЋЖЋ![]() ЗНЯђЩЯЃЌЕЦЫў
ЗНЯђЩЯЃЌЕЦЫў![]() дкЖЋББЗНЯђЩЯЃЌаЁУїбиКгАЖЯђЖЋаазп100УзжС
дкЖЋББЗНЯђЩЯЃЌаЁУїбиКгАЖЯђЖЋаазп100УзжС![]() ДІЃЌВтЕУДЫЪБЕЦЫў
ДІЃЌВтЕУДЫЪБЕЦЫў![]() дкББЦЋЮї
дкББЦЋЮї![]() ЗНЯђЩЯЃЌвбжЊКгСНАЖ
ЗНЯђЩЯЃЌвбжЊКгСНАЖ![]() ЃЎ
ЃЎ
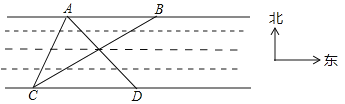
ЃЈ1ЃЉЧѓЙлВтЕу![]() ЕНЕЦЫў
ЕНЕЦЫў![]() ЕФОрРыЃЛ
ЕФОрРыЃЛ
ЃЈ2ЃЉЧѓЕЦЫў![]() ЃЌ
ЃЌ![]() жЎМфЕФОрРыЃЎ
жЎМфЕФОрРыЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЗДгГСЫМзЁЂввСНУћздааГЕАЎКУепЭЌЪБЦяГЕДг![]() ЕиЕН
ЕиЕН![]() ЕиНјаабЕСЗЪБааЪЛТЗГЬ
ЕиНјаабЕСЗЪБааЪЛТЗГЬ![]() ЃЈЧЇУзЃЉКЭааЪЛЪБМф
ЃЈЧЇУзЃЉКЭааЪЛЪБМф![]() ЃЈаЁЪБЃЉжЎМфЙиЯЕЕФВПЗжЭМЯёЃЌИљОнЭМЯёЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈаЁЪБЃЉжЎМфЙиЯЕЕФВПЗжЭМЯёЃЌИљОнЭМЯёЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
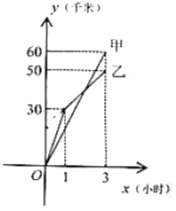
ЃЈ1ЃЉЧѓввЕФааЪЛТЗГЬ![]() КЭааЪЛЪБМф
КЭааЪЛЪБМф![]()
![]() жЎМфЕФКЏЪ§НтЮіЪНЃЛ
жЎМфЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉШчЙћМзЕФЫйЖШвЛжББЃГжВЛБфЃЌввдкЦяаа![]() аЁЪБжЎКѓгжвдЕк
аЁЪБжЎКѓгжвдЕк![]() аЁЪБЕФЫйЖШЦяааЃЌНсЙћСНШЫЭЌЪБЕНДя
аЁЪБЕФЫйЖШЦяааЃЌНсЙћСНШЫЭЌЪБЕНДя![]() ЕиЃЌЧѓ
ЕиЃЌЧѓ![]() ЁЂ
ЁЂ![]() СНЕижЎМфЕФОрРыЃЎ
СНЕижЎМфЕФОрРыЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com