
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲,乙,丙三名校排球队员每人10次垫球测试的成绩.测试规则为每次连续接球10个,每垫球到位1个记1分.

(1)若运动员丙测试成绩的平均数和众数都是7,则成绩统计表中a= ,b= ;
(2)若在三名队员中选择一位垫球成绩优秀且较为稳定的同学作为排球比赛的自由人,你认为选谁更合适?请用你所学过的统计量加以分析说明(参考数据:三人成绩的方差分别为![]() ,
,![]() ,
,![]() )
)
(3)训练期间甲、乙、丙三人之间进行随机传球游戏,先由甲传出球,经过三次传球,球回到甲手中的概率是多少?
【答案】(1)7;7 (2)见解析 (3)![]()
【解析】
(1)先根据众数的概念确定b的值,再利用平均数的概念列出求出a的值;
(2)计算出三人成绩的平均数,众数,结合方差的意义判断即可;
(3)画出树状图,然后根据概率公式列式进行计算即可得解.
(1)∵众数为7,
∴![]() ,
,
又平均数为7,
∴![]() ,
,
解得![]() ,
,
故答案为:7,7;
(2)甲的平均数为:![]() (分),众数是6(分);
(分),众数是6(分);
乙的平均数为:![]() (分),众数是7(分);
(分),众数是7(分);
丙的平均数为:![]() (分)众数是7(分);
(分)众数是7(分);
从平均数上看,乙和丙较高,从众数上看也是乙和丙较高;但是![]() <
<![]() ,
,
因此,综合考虑选乙更合适;
(3)画树状图如下:
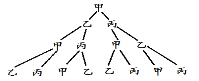
一共有8种可能,最后球传回到甲手中的情况有2种可能,
∴经过三次传球,球回到甲手中的概率是![]() .
.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】小明参加一个知识竞赛,该竞赛试题由10道选择题构成,每小题有四个选项,且只有一个选项正确.其给分标准为:答对一题得2分,答错一题扣1分,不答得0分,若10道题全部答对则额外奖励5分.小明对其中的8道题有绝对把握答对,剩下2道题完全不知道该选哪个选项.
(1)对于剩下的2道题,若小明都采用随机选择一个选项的做法,求两小题都答错的概率;
(2)从预期得分的角度分析,采用哪种做法解答剩下2道题更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() (k≠0)的图像与一次函数y=-x+b的图像在第一象限交于A、B两点,BC⊥x轴于点C,若△OBC的面积为2,且A点的纵坐标为4,B点的纵坐标为1.
(k≠0)的图像与一次函数y=-x+b的图像在第一象限交于A、B两点,BC⊥x轴于点C,若△OBC的面积为2,且A点的纵坐标为4,B点的纵坐标为1.
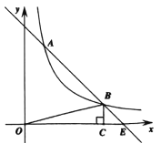
(1)求反比例函数、一次函数的表达式及直线AB与x轴交点E的坐标;
(2)已知点D(t,0)(t>0),过点D作垂直于x轴的直线,在第一象限内与一次函数y=-x+b的图像相交于点P,与反比函数![]() 上的图像相交于点Q,若点P位于点Q的上方,请结合函数图像直接写出此时t的取值范围.
上的图像相交于点Q,若点P位于点Q的上方,请结合函数图像直接写出此时t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
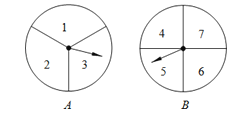
【题目】甲、乙两人用如图的两个分格均匀的转盘A、B做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:
(1)用列表格或画树状图的方法表示游戏所有可能出现的结果.
(2)求甲、乙两人获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某学校高中两个班的学生上学时步行、骑车、乘公交、乘私家车人数的扇形统计图,已知乘公交人数是乘私家车人数的2倍.若步行人数是18人,则下列结论正确的是( )

A. 被调查的学生人数为90人
B. 乘私家车的学生人数为9人
C. 乘公交车的学生人数为20人
D. 骑车的学生人数为16人
查看答案和解析>>
科目:初中数学 来源: 题型:
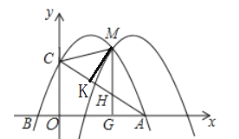
【题目】如图,抛物线y=ax2+bx+2(a≠0)与x轴交于A(4,0)、B(﹣1,0)两点,与y轴交于点C.
(1)求抛物线的表达式和顶点坐标;
(2)把(1)中所求出的抛物线记为C1,将C1向右平移m个单位得到抛物线C2,C1与C2的在第一象限交点为M,过点M作MK![]() 于K,MG⊥x轴于点G,交线段AC于点H,连接CM.
于K,MG⊥x轴于点G,交线段AC于点H,连接CM.
①求线段MK长度的最大值;
②当△CMH为等腰三角形时,求抛物线向右平移的距离m和此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
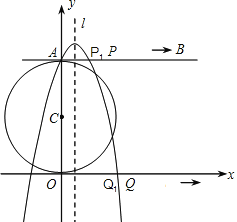
【题目】如图,在平面直角坐标系中,以点C(0,4)为圆心,半径为4的圆交y轴正半轴于点A,AB是⊙C的切线.动点P从点A开始沿AB方向以每秒1个单位长度的速度运动,点Q从O点开始沿x轴正方向以每秒4个单位长度的速度运动,且动点P、Q从点A和点O同时出发,设运动时间为t(秒).
(1)当t=1时,得到P1、Q1,求经过A、P1、Q1三点的抛物线解析式及对称轴l;
(2)当t为何值时,直线PQ与⊙C相切?并写出此时点P和点Q的坐标;
(3)在(2)的条件下,抛物线对称轴l上存在一点N,使NP+NQ最小,求出点N的坐标并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC⊥AB于点B,连接OC交⊙O于点E,弦AD∥OC,弦DF⊥AB于点G.
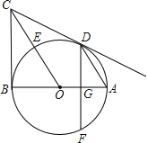
(1)求证:点E是![]() 的中点;
的中点;
(2)求证:CD是⊙O的切线;
(3)若sin∠BAD=![]() ,⊙O的半径为5,求DF的长.
,⊙O的半径为5,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如表是一个4×4(4行4列共16个“数”组成)的奇妙方阵,从这个方阵中选四个“数”,而且这四个“数”中的任何两个不在同一行,也不在同一列,有很多选法,把每次选出的四个“数”相加,其和是定值,则方阵中第三行三列的“数”是( )
30 |
| 2 | 22 |
﹣3 | ﹣2 | ﹣ | 0 |
|﹣5| | 6 | 23 | |
( | 4 |
| ( |
A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com