
【题目】在正方形ABCD中,E是CD边上一点(CE>DE),AE,BD交于点F.
(1)如图1,过点F作GH⊥AE,分别交边AD,BC于点G,H.
求证:∠EAB=∠GHC;
(2)AE的垂直平分线分别与AD,AE,BD交于点P,M,N,连接CN.
①依题意补全图形;
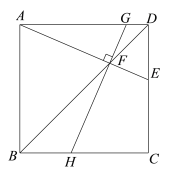
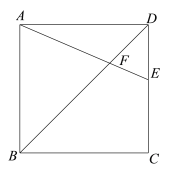
图1 备用图
②用等式表示线段AE与CN之间的数量关系,并证明.
【答案】(1)详见解析;(2)①补全图形,如图所示.②![]() .详见解析
.详见解析
【解析】
(1)根据正方形的性质,有AD∥BC,∠BAD=90°,得到∠AGH=∠GHC,再根据GH⊥AE,得到∠EAB=∠AGH,即可证明.
(2)①根据垂直平分线的作法步骤进行即可.
②连接AN,连接EN并延长,交AB边于点Q,根据正方形的性质,得到NA=NC,∠1=∠2,再根据垂直平分线的性质,得到NA=NE,进而得到NC=NE,∠3=∠4,在正方形ABCD中,BA∥CE,∠BCD=90°,得到∠AQE=∠4,∠1+∠AQE=∠2+∠3=90°,∠ANE=∠ANQ=90°,最后在Rt△ANE中,即可求解.
(1)证明:在正方形ABCD中,AD∥BC,∠BAD=90°,
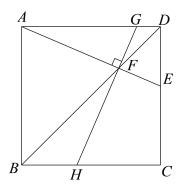
∴∠AGH=∠GHC.
∵GH⊥AE,
∴∠EAB=∠AGH.
∴∠EAB=∠GHC.
(2)①补全图形,如图所示.
②![]() .
.
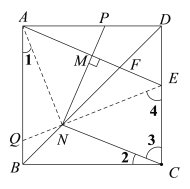
证明:连接AN,连接EN并延长,交AB边于点Q.
∵四边形ABCD是正方形,
∴点A,点C关于BD对称.
∴NA=NC,∠1=∠2.
∵PN垂直平分AE,
∴NA=NE.
∴NC=NE.
∴∠3=∠4.
在正方形ABCD中,BA∥CE,∠BCD=90°,
∴∠AQE=∠4.
∴∠1+∠AQE=∠2+∠3=90°.
∴∠ANE=∠ANQ=90°.
在Rt△ANE中,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】为了解某地区企业信息化发展水平,从该地区中随机抽取50家企业调研,针对体现企业信息化发展水平的A和B两项指标进行评估,获得了它们的成绩(十分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.A项指标成绩的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
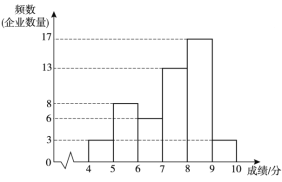
b.A项指标成绩在![]() 这一组的是:
这一组的是:
7.2 7.3 7.5 7.67 7.7 7.71 7.75 7.82 7.86 7.9 7.92 7.93 7.97
c.![]() 两项指标成绩的平均数、中位数、众数如下:
两项指标成绩的平均数、中位数、众数如下:
平均数 | 中位数 | 众数 | |
A项指标成绩 | 7.37 | m | 8.2 |
B项指标成绩 | 7.21 | 7.3 | 8 |
根据以上信息,回答下列问题:
(1)写出表中m的值
(2)在此次调研评估中,某企业A项指标成绩和B项指标成绩都是7.5分,该企业成绩排名更靠前的指标是______________(填“A”或“B”),理由是_____________;
(3)如果该地区有500家企业,估计A项指标成绩超过7.68分的企业数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师将“校园诗词大赛”所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图,部分信息如下:
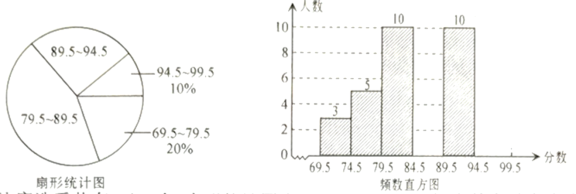
(1)本次比赛选手共有_ 人,扇形统计图中“![]() ”这一组人数占总参赛人数的百分比为_ ,频数直方图中“
”这一组人数占总参赛人数的百分比为_ ,频数直方图中“![]() ”这一组的人数为__ ;
”这一组的人数为__ ;
(2)赛前规定,成绩由高到低前![]() 的参赛选手获奖某参赛选手的比赛成绩为
的参赛选手获奖某参赛选手的比赛成绩为![]() 分,试判断他能否获奖,并说明理由;
分,试判断他能否获奖,并说明理由;
(3)成绩前四名是![]() 名男生和
名男生和![]() 名女生,若从他们中任选
名女生,若从他们中任选![]() 人作为全区“诗词大会”重点培训对象,试求恰好选中
人作为全区“诗词大会”重点培训对象,试求恰好选中![]() 男
男![]() 女的概率.
女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2![]() ,点A的纵坐标为4.
,点A的纵坐标为4.
(1)求该反比例函数和一次函数的解析式;
(2)连接MC,求四边形MBOC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医院医生为了研究该院某种疾病的诊断情况,需要调查来院就诊的病人的两个生理指标![]() ,
,![]() ,于是他分别在这种疾病的患者和非患者中,各随机选取20人作为调查对象,将收集到的数据整理后,绘制统计图如下:
,于是他分别在这种疾病的患者和非患者中,各随机选取20人作为调查对象,将收集到的数据整理后,绘制统计图如下:
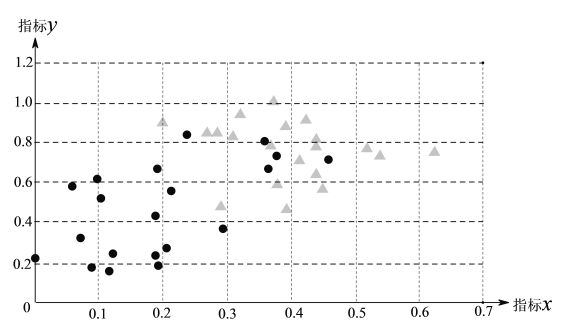
注“●”表示患者,“▲”表示非患者.
根据以上信息,回答下列问题:
(1)在这40名被调查者中,
①指标![]() 低于0.4的有 人;
低于0.4的有 人;
②将20名患者的指标![]() 的平均数记作
的平均数记作![]() ,方差记作
,方差记作![]() ,20名非患者的指标
,20名非患者的指标![]() 的平均数记作
的平均数记作![]() ,方差记作
,方差记作![]() ,则
,则![]()
![]() ,
,![]()
![]() (填“>”,“=”或“<”);
(填“>”,“=”或“<”);
(2)来该院就诊的500名未患这种疾病的人中,估计指标![]() 低于0.3的大约有 人;
低于0.3的大约有 人;
(3)若将“指标![]() 低于0.3,且指标
低于0.3,且指标![]() 低于0.8”作为判断是否患有这种疾病的依据,则发生漏判的概率多少.
低于0.8”作为判断是否患有这种疾病的依据,则发生漏判的概率多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“在已知三角形的一边上取一点,使得这点到这个三角形的另外两边的距离相等”的尺规作图过程:
已知:△ABC.
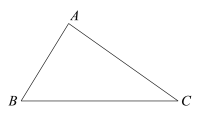
求作:点D,使得点D在BC边上,且到AB,AC边的距离相等.
作法:如图,
作∠BAC的平分线,交BC于点D.则点D即为所求.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形 (保留作图痕迹);
(2)完成下面的证明.
证明:作DE⊥AB于点E,作DF⊥AC于点F,
∵AD平分∠BAC,
∴ = ( ) (填推理的依据) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,E是CD边上一点(CE>DE),AE,BD交于点F.
(1)如图1,过点F作GH⊥AE,分别交边AD,BC于点G,H.
求证:∠EAB=∠GHC;
(2)AE的垂直平分线分别与AD,AE,BD交于点P,M,N,连接CN.
①依题意补全图形;
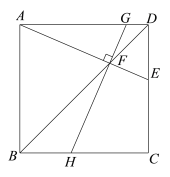

图1 备用图
②用等式表示线段AE与CN之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1,E1,E2,C2,E3,E4,C3……在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3……,则正方形A2020B2020C2020D2020的边长是( )
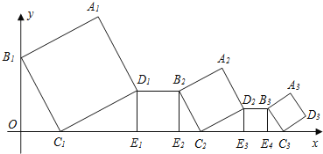
A.(![]() )2017B.(
)2017B.(![]() )2018C.(
)2018C.(![]() )2019D.(
)2019D.(![]() )2020
)2020
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com