
【题目】如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
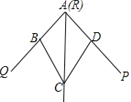
A. SAS B. ASA C. AAS D. SSS
科目:初中数学 来源: 题型:
【题目】如图,点B和点C分别为∠MAN两边上的点,AB=AC.

(1)按下列语句画出图形:(要求不写作法,保留作图痕迹)
① AD⊥BC,垂足为D;
② ∠BCN的平分线CE与AD的延长线交于点E;
③ 连结BE.
(2)在完成(1)后不添加线段和字母的情况下,请你写出除△ABD≌△ACD外的两对全等三角形: ≌ , ≌ ;并选择其中的一对全等三角形予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在墙壁上用两个钉子就能固定一根横放的木条,这样做根据的道理是( )
A. 两点确定一条直线 B. 两点确定一条线段
C. 两点之间,直线最短 D. 两点之间,线段最短
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】使用计算器计算各式:6×7= ,66×67= ,666×667= ,6 666×6 667= .
(1)根据以上结果,你发现了什么规律?
(2)依照你发现的规律,不用计算器,你能直接写出666 666×666 667的结果吗?请你试一试.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图3,直线AB、CD相交于点O,∠AOE=90°,从给出的A、B、C三个答案中选择适当答案填空.

(1)∠1与∠2的关系是( )
(2)∠3与∠4的关系是( )
(3)∠3与∠2的关系是( )
(4)∠2与∠4的关系是( )
A.互为补角 B.互为余角 C.即不互补又不互余
查看答案和解析>>
科目:初中数学 来源: 题型:
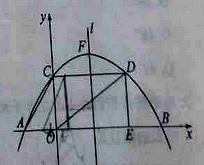
【题目】(2016山东省聊城市第25题)如图,已知抛物线y=ax2+bx+c经过点A(﹣3,0),B(9,0)和C(0,4).CD垂直于y轴,交抛物线于点D,DE垂直与x轴,垂足为E,l是抛物线的对称轴,点F是抛物线的顶点.
(1)求出二次函数的表达式以及点D的坐标;
(2)若Rt△AOC沿x轴向右平移到其直角边OC与对称轴l重合,再沿对称轴l向上平移到点C与点F重合,得到Rt△A1O1F,求此时Rt△A1O1F与矩形OCDE重叠部分的图形的面积;
(3)若Rt△AOC沿x轴向右平移t个单位长度(0<t≤6)得到Rt△A2O2C2,Rt△A2O2C2与Rt△OED重叠部分的图形面积记为S,求S与t之间的函数表达式,并写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=a![]() +bx+6(a≠0)的图象与x轴交于A、B两点(点A在点B的左侧),点A、点B的横坐标是方程
+bx+6(a≠0)的图象与x轴交于A、B两点(点A在点B的左侧),点A、点B的横坐标是方程![]() -4x-12=0的两个根.
-4x-12=0的两个根.
(1)求出该二次函数的表达式及顶点坐标;
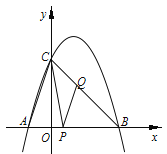
(2)如图,连接AC、BC,点P是线段OB上一个动点(点P不与点O、B重合),过点P作PQ∥AC交BC于点Q,当△CPQ的面积最大时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com