
����Ŀ������ABC�У���ACB=90�㣬AC=BC��ֱ��MN������C����AD��MN��D��BE��MN��E��
��1����ֱ��MN�Ƶ�C��ת��ͼ1��λ��ʱ����֤���١�ADC�ա�CEB����DE=AD+BE��
��2����ֱ��MN�Ƶ�C��ת��ͼ2��λ��ʱ����֤��DE=AD��BE��
��3����ֱ��MN�Ƶ�C��ת��ͼ3��λ��ʱ������DE��AD��BE���������ĵ�����ϵ����д�����������ϵ��������֤����
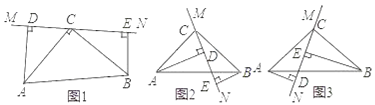
���𰸡���1��֤������������2��֤������������3��DE=BE��AD��
����������1������֪AC=BC����ADC=��CEB=90�㣬���û����ϵ��֤��DAC=��ECB����֤��ACD�ա�CBE����AD=CE��CD=BE����AD+BE=CE+CD=DE����2����ʱ�����С�ACD�ա�CBE��AD=CE��CD=BE�������߶εĺͲ��ϵ��DE=AD-BE��
֤������1���ߡ�ADC=��ACB=��BEC=90�㣬
���CAD+��ACD=90�㣬��BCE+��CBE=90�㣬��ACD+��BCE=90�㣮
���CAD=��BCE��
��AC=BC��
���ADC�ա�CEB��
��CE=AD��CD=BE��
��DE=CE+CD=AD+BE��
��2��DE=AD��BE
֤�����ߡ�ADC=��CEB=��ACB=90�㣬
���ACD=��CBE��
�֡�AC=BC��
���ACD�ա�CBE��
��CE=AD��CD=BE��
��DE=CE��CD=AD��BE��
��3��DE=BE��AD����AD=BE��DE��BE=AD+DE�ȣ���
��֤�á�ACD�ա�CBE��
��AD=CE��DC=BE��
��DE=CD- CE =BE��AD��
���㾦�����⿼��������ת��Ѱ��֤��������ȫ�ȵ��������ؼ�������ȫ�������ζ�Ӧ�߶���ȣ����й��߶ν���ת����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
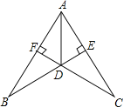
����Ŀ����ͼ��BE��AC��CF��AB�ڵ�E��F��BE��CF���ڵ�D��DE=DF������AD��
��֤����1����FAD=��EAD��2��BD=CD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������ε��ڽǺ���720�㣬���������ǣ�������
A. ����� B. ������ C. �߱��� D. �˱���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У���E��DA���ӳ����ϣ���F��BC���ӳ����ϣ���BE��FD����֤����ABE=��CDF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������(-xy)3��(7xy2-9x2y)�Ľ����ȷ����( )
A. -7x2y5+9x3y4 B. 7x2y5-9x3y4 C. -7x4y5+9x5y4 D. 7x4y5+9x5y4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
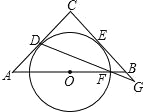
����Ŀ����ͼ����֪��ABC��AC=BC����C=90�㣮O��AB���е㣬��O��AC��BC�ֱ������ڵ�D���E����F�ǡ�O��AB��һ�����㣬��DF���ӳ���CB���ӳ����ڵ�G�����CDG= ����AB=![]() ����BG= ��
����BG= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
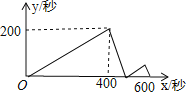
����Ŀ���ס���������ͬһֱ�ߵ�·��ͬ��㡢ͬ����ͬʱ�������ֱ��Բ�ͬ���ٶ������ܲ�1500�ף����׳�����200��ʱ����ͣ�����Ⱥ��ң��ס��һ�Ϻ����˷ֱ���ԭ�����ٶȼ��������յ㣬�ȵ��յ�������յ���Ϣ�����ܲ������������У��ס������˵ľ���y���ף����ҳ�����ʱ��x���룩֮��Ĺ�ϵ��ͼ��ʾ������յ�ʱ�������� ______�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������о��е���ѧ�������ᄊ�˶����ϣ��μ��������ߵ�15���˶�Ա�ijɼ����±���ʾ��
�ɼ���m�� | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
���� | 1 | 2 | 4 | 3 | 3 | 2 |
��Щ�˶�Ա���߳ɼ�����λ���������ֱ��ǣ�������
A. 1.70��1.65 B. 1.70��1.70 C. 1.65��1.70 D. 3��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����C��DΪ��ԲO�ϵ����㣬CD��AB������C��CE��AD����AD���ӳ����ڵ�E��tanA=![]() ��
��
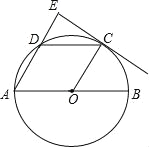
��1����֤��CE�ǡ�O�����ߣ�
��2�������ı���AOCD��ʲô������ı��Σ���֤����IJ��룮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com