
如图,抛物线 交
交 轴于
轴于 两点(
两点( 的左侧),交
的左侧),交 轴于点
轴于点 ,顶点为
,顶点为 。
。

(1)求点 的坐标;
的坐标;
(2)求四边形 的面积;
的面积;
(3)抛物线上是否存在点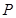 ,使得
,使得 ,若存在,请求出点
,若存在,请求出点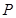 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
(1) A(-1,0);B(3,0);C(0,3);(2)9;(3) 存在这样的点P,P点的坐标为(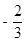 ,
,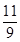 )或(
)或(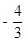 ,
,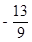 ).
).
【解析】
试题分析:(1)在抛物线的解析式中,令x=0可以求出点C的坐标,令x=0可以求出A、B点的坐标.
(2)过D作DE⊥AB,垂足为E,则四边形ABDC的面积就是: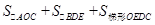
(3)根据条件判定△BCD是直角三角形,再依据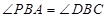 求出
求出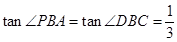 .设P点坐标为(m,-m2+2m+3),分两种情况讨论:(1)当P点在x 轴上方时,(2)当P点在x轴下方时,解直角三角形即可求出m的值,从而确定点P的坐标.
.设P点坐标为(m,-m2+2m+3),分两种情况讨论:(1)当P点在x 轴上方时,(2)当P点在x轴下方时,解直角三角形即可求出m的值,从而确定点P的坐标.
试题解析:(1)当x=0时,y=-x2+2x+3=3;
当y=0时,0=-x2
解得:x1=-1、x2=3;
故A(-1,0);B(3,0);C(0,3).
(2)
∴D点坐标为(1,4)
过点D作DE⊥x轴于E
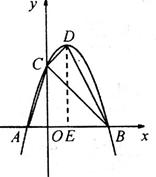
∴OE=1,DE=4
∴BE=OB-OE=2
∵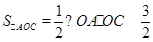 ,
, ,
,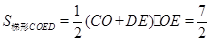
∴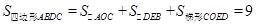
(3)假设存在这样的点P
过点C作CF⊥DE于F
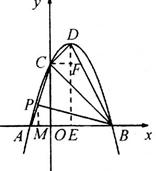
∴CF=1,DF=1
∴∠DCF=45°,CD=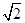
∵OC=3=OB,
∴∠CBO=45°,BC=
∵CF∥x轴
∴∠FCB=∠CBO=45°,
∴∠DCB=90°
在Rt△BCD中,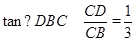
∴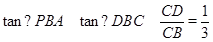
设P点坐标为(m,-m2+2m+3),
过点P作PM⊥AB于M
当P点在x轴上方时,PM=-m2+2m+3,BM=3-m
在Rt△PBM中,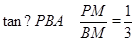 ,即
,即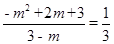
∴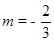 或
或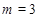 (舍去)
(舍去)
∴P点坐标为(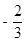 ,
,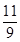 )
)
当P点在x轴下方时,PM=-m2-2m-3,BM=3-m
在Rt△PBM中,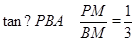 ,即
,即
∴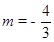 或
或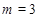 (舍去)
(舍去)
∴P点坐标为(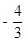 ,
,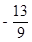 )
)
综上,存在这样的点P,P点的坐标为(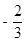 ,
,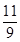 )或(
)或(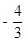 ,
,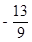 )
)
考点: 二次函数综合题.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
如图,已知抛物线 交 轴于A、B两点,交 轴于点C,抛物线的对称轴交 轴于点E,点B的坐标为( ,0).
(1)求抛物线的对称轴及点A的坐标;
(2)在平面直角坐标系 中是否存在点P,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由;
(3)连结CA与抛物线的对称轴交于点D,在抛物线上是否存在点M,使得直线CM把四边形DEOC分成面积相等的两部分?若存在,请求出直线CM的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线与 轴交于
轴交于![]() (
(![]() ,0)、
,0)、![]() (
(![]() ,0)两点,且
,0)两点,且![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其中
,其中![]() 是方程
是方程![]() 的两个根。(14分)
的两个根。(14分)
(1)求抛物线的解析式;
 (2)点
(2)点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() ∥
∥![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,当
,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
(3)点![]() 在(1)中抛物线上,
在(1)中抛物线上,
点 为抛物线上一动点,在
为抛物线上一动点,在![]() 轴上是
轴上是
否存在点 ,使以
,使以![]() 为顶
为顶
点的四边形是平行四边形,如果存在,
求出所有满足条件的点![]() 的坐标,
的坐标,
若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
 轴交于
轴交于 (
( ,0)、
,0)、 (
( ,0)两点,且
,0)两点,且 ,与
,与 轴交于点
轴交于点 ,其中
,其中 是方程
是方程 的两个根。
的两个根。 是线段
是线段 上的一个动点,过点
上的一个动点,过点 作
作 ∥
∥ ,交
,交 于点
于点 ,连接
,连接 ,当
,当 的面积最大时,求点
的面积最大时,求点 的坐标;
的坐标; 在(1)中抛物线上,点
在(1)中抛物线上,点 为抛物线上一动点,在
为抛物线上一动点,在 轴上是否存在点
轴上是否存在点 ,使以
,使以 为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点
为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点 的坐标,若不存在,请说明理由。
的坐标,若不存在,请说明理由。查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(山东莱芜) 题型:解答题
(本题满分12分)
如图,在平面直角坐标系中,已知抛物线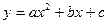 交
交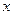 轴于
轴于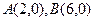 两点,交
两点,交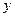 轴于点
轴于点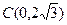 .
.
(1)求此抛物线的解析式; (2)若此抛物线的对称轴与直线
(2)若此抛物线的对称轴与直线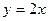 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交 轴于点E、F两点,求劣弧EF的长;
轴于点E、F两点,求劣弧EF的长;
(3)P为此抛物线在第二象限图像上的一点,PG垂直于 轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(四川内江) 题型:解答题
(本题满分12分)
如图,在平面直角坐标系中,已知抛物线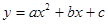 交
交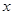 轴于
轴于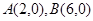 两点,交
两点,交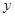 轴于点
轴于点 .
.
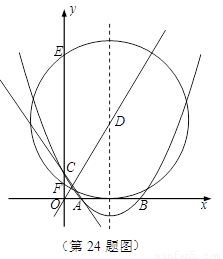
(1)求此抛物线的解析式;
 (2)若此抛物线的对称轴与直线
(2)若此抛物线的对称轴与直线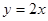 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交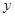 轴于点E、F两点,求劣弧EF的长;
轴于点E、F两点,求劣弧EF的长;
(3)P为此抛物线在第二象限图像上的一点,PG垂直于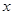 轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com