
分析 画出函数图象,找出直线与函数D(-x2+1,x-1,-x-1)的图象有一个、两个、三个交点的临界点,再结合图形即可得出结论.
解答 解:画出函数图象,如图所示.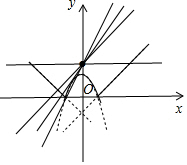
当直线y=mx+$\frac{3}{2}$与y=x-1平行,即m=1时,
直线y=mx+$\frac{3}{2}$(m>0)与函数D(-x2+1,x-1,-x-1)的图象只有一个交点;
当直线y=mx+$\frac{3}{2}$与x轴平行,即m=0时,
直线y=mx+$\frac{3}{2}$(m>0)与函数D(-x2+1,x-1,-x-1)的图象有两个交点;
当直线y=mx+$\frac{3}{2}$过点(-1,0)时,有-m+$\frac{3}{2}$=0,即m=$\frac{3}{2}$,
此时直线y=mx+$\frac{3}{2}$(m>0)与函数D(-x2+1,x-1,-x-1)的图象只有一个交点;
当直线y=mx+$\frac{3}{2}$与y=-x2+1相切时,方程x2+mx+$\frac{1}{2}$=0有两个相等的实数根,
∴△=m2-4×1×$\frac{1}{2}$=0,m=$\sqrt{2}$,
此时直线y=mx+$\frac{3}{2}$(m>0)与函数D(-x2+1,x-1,-x-1)的图象有两个交点.
综上所述:当m=$\frac{3}{2}$、m=$\sqrt{2}$或0<m<1时,直线y=mx+$\frac{3}{2}$(m>0)与函数D(-x2+1,x-1,-x-1)的图象有且只有两个交点.
故答案为:m=$\frac{3}{2}$、m=$\sqrt{2}$或0<m<1.
点评 本题考查了一次函数的性质、二次函数的性质以及数形结合,画出函数图象,利用数形结合是解题的关键.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 400d cm | B. | 300d cm | C. | 304d cm | D. | 301d cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
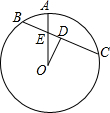 如图,D是⊙O弦BC的中点,A是⊙O上的一点,OA与BC交于点E,已知AO=8,BC=12.
如图,D是⊙O弦BC的中点,A是⊙O上的一点,OA与BC交于点E,已知AO=8,BC=12.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 文具店 | B. | 玩具店 | C. | 文具店西40米处 | D. | 玩具店西60米处 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-3)2=3 | B. | (x+3)2=3 | C. | (x-6)2=30 | D. | (x+6)2=30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com