练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在平行四边形ABCD中，∠ABC=45°，E、F分别在CD和BC的延长线上，AE∥BD，∠EFC=30°， AB=2.求CF的长．


    解：∵四边形ABCD是平行四边形，

    ∴AB∥DC，AB=DC，

    ∵AE∥BD，

    ∴四边形ABDE是平行四边形，

    ∴AB=DE=CD，  

    即D为CE中点，

    ∵AB=2，∴CE=4，   

    又∵AB∥CD，∴∠ECF=∠ABC=45°，

    过点E作EH⊥BF于点H，

    ∵CE=4，∠ECF=45°，∴EH=CH=2，

    ∵∠EFC=30°，∴ FH=2，∴ CF=2+2


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    已知关于的一元二次方程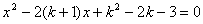有两个不相等的实数根．

    （1）求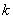的取值范围；

    （2）当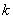取最小的整数时，求抛物线  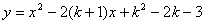    的顶点坐标以及它与轴的交点坐标；

    （3）将(2)中求得的抛物线在轴下方的部分沿轴翻折到轴上方，图象的其余部分不变，得到一个新图象．请你画出这个新图象，并求出新图象与直线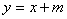有三个不同公共点时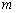的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解不等式：.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在下列某品牌T恤的四个洗涤说明图案的设计中，没有运用旋转或轴对称知识的是

                                                                

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    问题：在中，，∠A=100°，BD为∠B 的平分线，探究AD、BD、BC之间的数量关系.

    请你完成下列探究过程：

    （1）观察图形，猜想AD、BD、BC之间的数量关系为                         .

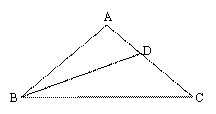    （2）在对（1）中的猜想进行证明时，当推出∠ABC=∠C=40°后，可进一步推出∠ABD=∠DBC=           度.

    （3）为了使同学们顺利地解答本题（1）中的猜想，小强同学提供了一种探究的思路：在BC上截取BE=BD，连接DE,在此基础上继续推理可使问题得到解决.你可以参考小强的思路，画出图形，在此基础上对（1）中的猜想加以证明.也可以选用其它的方法证明你的猜想.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    小明用自制的直角三角形纸板DEF测量树AB的高度．测量时，使直角边DE保持水平状态，其延长线交AB于点G；使斜边DF与点A在同一条直线上．测得边DE离地面的高度GB为1.4m，点D到AB的距离DG为6m（如图所示）．已知DE=30cm，EF=20cm，那么树AB的高度等于

    A．4 m          B．5.4 m           C．9 m           D．10.4 m

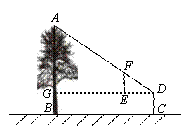
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知：抛物线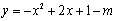与x轴相交于A、B两点，与y轴相交于点C，其中

    点C的坐标是（0，3），顶点为点D，联结CD，抛物线的对称轴与x轴交于点E．

    （1）求m的值；

    （2）求∠CDE的度数；

    （3）在抛物线对称轴的右侧部分上是否存在一点P，使得△PDC是等腰三角形？如果

    存在，求出符合条件的点P的坐标；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，⊙O的半径是5，△ABC是⊙O的内接三角形，过圆心O分别作AB、BC、AC的垂线，垂足为E、F、G，连接EF． 若OG＝2，则EF为          ．

    查看答案和解析>>

    同步练习册答案