
【题目】已知三角形的第一条边的长是![]() ,第二条边长是第一条边长的2倍少3,第三条边比第二条边短5。
,第二条边长是第一条边长的2倍少3,第三条边比第二条边短5。
(1)用含![]() 、
、![]() 的式子表示这个三角形的周长;
的式子表示这个三角形的周长;
(2)当![]() ,
,![]() 时,求这个三角形的周长;
时,求这个三角形的周长;
(3)当![]() ,三角形的周长为 39时,求各边长。
,三角形的周长为 39时,求各边长。
科目:初中数学 来源: 题型:
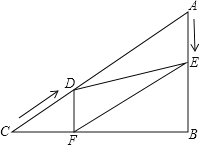
【题目】如图所示,在Rt△ABC中,∠B=90°,AC=100cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤25).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:四边形AEFD是平行四边形;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
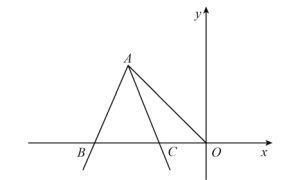
【题目】在平面直角坐标系中,点 ![]() 的坐标为
的坐标为![]() ,以 A 为顶点的
,以 A 为顶点的![]() 的两边始终与
的两边始终与 ![]() 轴交于
轴交于 ![]() 、
、![]() 两点(
两点(![]() 在
在 ![]() 左面),且
左面),且![]() .
.
(1)如图,连接![]() ,当
,当 ![]() 时,试说明:
时,试说明:![]() .
.
(2)过点 ![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,当
,当![]() 时,将
时,将![]() 沿
沿![]() 所在直线翻折,翻折后边
所在直线翻折,翻折后边![]() 交
交 ![]() 轴于点
轴于点 ![]() ,求点
,求点 ![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在直线AB上,点A1,A2,A3,…在射线OA上,点B1,B2,B3,…在射线OB上,图中的每一个实线段和虚线段的长均为1个单位长度.一个动点M从O点出发,按如图所示的箭头方向沿着实线段和以O为圆心的半圆匀速运动,速度为每秒1个单位长度.按此规律,则动点M到达A101点处所需时间为( )秒.

A. 5050π B. 5050π+101 C. 5055π D. 5055π+101
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=65°,∠2=65°,∠3=115°.试说明:DE∥BC,DF∥AB.根据图形,完成下面的推理:

因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以______________∥ ( ).
因为AB与DE相交,
所以∠1=∠4( ).
所以∠4=65°.
又因为∠3=115°,
所以∠3+∠4=180°.
所以 ∥ ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(如图(1),一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在线段OP上滑动,将窗户OM按图示方向向内旋转45°到达ON位置,如图(2),此时,点A、C的对应位置分别是点B、D,测量出∠ODB为37°,点D到点O的距离为28cm. 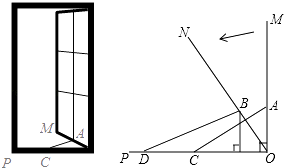
(1)求B点到OP的距离.
(2)求滑动支架AC的长. (参考数据:sin37°= ![]() ,cos37°=
,cos37°= ![]() ,tan37°=
,tan37°= ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解决问题,
例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
解:∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0,n﹣3=0
∴m=﹣3,n=3
问题(1)若x2+2y2﹣2xy+4y+4=0,求xy的值.
(2)已知a,b,c是△ABC的三边长,满足a2+b2=10a+8b﹣41,且c是△ABC中最长的边,求c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB,用尺规按要求作图.(用黑色水笔描粗作图痕迹,不要求写作法)
(1)延长线段AB到C,使BC=AB;
(2)延长线段BA到D,使AD=2AB;
(3)若AB=2cm,则BD=__________cm,CD=__________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程(n-2)x2m+3+3y5|n|-9=4.
(1)若方程是二元一次方程,求m2+n2的值;
(2)若方程是一元一次方程,求m,n的值或取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com