
分析 (1)根据题意列出方程$\frac{x+2}{2}$=$\frac{x-1}{3}$-2,解方程即可;
(2)利用题中的新定义首先得到2*x=1-$\frac{1}{3}$x,那么原方程可化为1-$\frac{1}{3}$(1-$\frac{1}{3}$x)=$\frac{1}{2}$-$\frac{1}{3}$x,求出方程的解即可.
解答 解:(1)根据题意,得$\frac{x+2}{2}$=$\frac{x-1}{3}$-2,
去分母,得3(x+2)=2(x-1)-12,
去括号,得3x+6=2x-2-12,
移项合并,得x=-20;
(2)根据题中的新定义化简2*(2*x)=1*x得:2*(1-$\frac{1}{3}$x)=$\frac{1}{2}$-$\frac{1}{3}$x,
即1-$\frac{1}{3}$(1-$\frac{1}{3}$x)=$\frac{1}{2}$-$\frac{1}{3}$x,
去分母得:6-2(2-$\frac{1}{3}$x)=3-2x,
去括号得:6-4+$\frac{2}{3}$x=3-2x,
去分母得:6+2x=9-6x,
移项合并得:8x=3,
解得:x=$\frac{3}{8}$.
点评 此题考查了一元一次方程的应用及解一元一次方程,根据题意列出方程是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
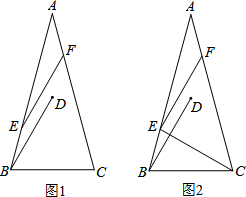 在△ABC 中,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上.
在△ABC 中,AB=AC,∠A=30°,将线段BC绕点B逆时针旋转60°得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
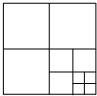 如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,…,请你根据以上操作方法得到的正方形的个数的规律完成各题.
如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪成四个小正方形,如此继续下去,…,请你根据以上操作方法得到的正方形的个数的规律完成各题.| 操作次数N | 1 | 2 | 3 | 4 | 5 | … | n |
| 正方形个数 | 4 | 7 | 10 | an |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
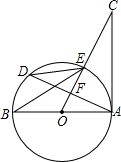 如图,AB是⊙O的直径,AD是弦,OC⊥AD于F,交⊙O于点E,∠BED=∠C.若OA=6,AC=8,则cos∠D=$\frac{2\sqrt{5}}{5}$.
如图,AB是⊙O的直径,AD是弦,OC⊥AD于F,交⊙O于点E,∠BED=∠C.若OA=6,AC=8,则cos∠D=$\frac{2\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com