
| 时间 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 45 |
| 人数 | 3 | 3 | 6 | 12 | 2 | 2 | 1 | 1 |
分析 (1)根据中位数和众数的含义和求法,写出这组数据的中位数和众数即可.
(2)首先求出这30名同学每天上学一共要用多少时间;然后用它除以30,求出平均时间是多少即可.
解答 解:(1)根据统计表,可得
这组数据的第15个数、第16个数都是20,
∴这组数据的中位数是:
(20+20)÷2
=40÷2
=20
这组数据的众数是20.
(2)(5×3+10×3+15×6+20×12+25×2+30×2+35×1+45×1)÷30
=(15+30+90+240+50+60+35+45)÷30
=565÷30
=18$\frac{5}{6}$(分钟)
答:这30名同学每天上学的平均时间是18$\frac{5}{6}$分钟.
点评 此题主要考查了平均数、中位数、众数的含义和求法,要熟练掌握.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 贵州省清镇体育训练基地,有一块边长为(2m+3n)米的正方形土地(如图所示),现准备在这块正方形土地上修建一个长为(2m+2n)米,宽为(m+n)米的长方形游泳池,剩余部分(图中阴影部分)修建成休息区域.
贵州省清镇体育训练基地,有一块边长为(2m+3n)米的正方形土地(如图所示),现准备在这块正方形土地上修建一个长为(2m+2n)米,宽为(m+n)米的长方形游泳池,剩余部分(图中阴影部分)修建成休息区域.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
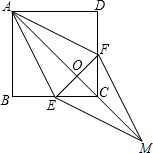 已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF,连结AC交EF于点O,延长OC至点M,使OM=OA,连结EM,FM.
已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF,连结AC交EF于点O,延长OC至点M,使OM=OA,连结EM,FM.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com