
【题目】阅读理解:如图①所示,在平面内选一定点O,引一条有方向的射线ON,再选定一个单位长度,那么平面上任一点M的位置可由OM的长度m与∠MON的度数θ确定,有序数对(m,θ)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图②的极坐标系下,如果正六边形的边长为2,有一边OA在射线ON上,则正六边形的顶点C的极坐标应记为( )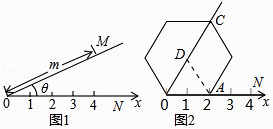
A.(4,60°)
B.(4,45°)
C.(2 ![]() ,60°)
,60°)
D.(2 ![]() ,50°)
,50°)
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】小明身高为1.6米,通过地面上的一块平面镜C,刚好能看到前方大树的树梢E,此时他测得俯角为45度,然后他直接抬头观察树梢E,测得仰角为30度.求树的高度.(结果保留根号) 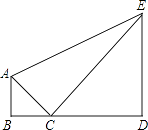
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E. 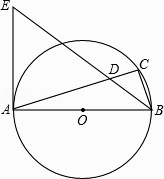
(1)∠ACB=°,理由是:;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE= ![]() ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).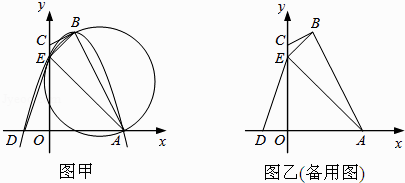
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;
(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是绝对值等于4的负数,b是最小的正整数,c的倒数的相反数是﹣2,
(1)求a,b,c的值;
(2)求:4a2b3﹣[2abc+(5a2b3﹣7abc)﹣a2b3].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目最喜爱的情况,随机调查了若干名学生,根据调查数据进行整理,绘制了如下的不完整统计图. 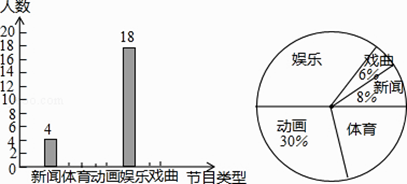
请你根据以上的信息,回答下列问题:
(1)本次共调查了名学生,其中最喜爱戏曲的有人;在扇形统计图中,最喜爱体育的对应扇形的圆心角大小是 .
(2)根据以上统计分析,估计该校2000名学生中最喜爱新闻的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于B,与直线y=x交于点C.
与x轴交于点A,与y轴交于B,与直线y=x交于点C.
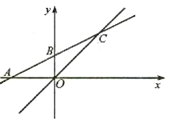
(1)求A、B、C三点的坐标;
(2)求△AOC的面积;
(3)已知点P是x轴正半轴上的一点,若△COP是等腰三角形,直接写点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店第一次用500元购进钢笔若干支,第二次又用500元购进该款钢笔,但这次每支的进价是第一次进价的 ![]() 倍,购进数量比第一次少了25支.
倍,购进数量比第一次少了25支.
(1)求第一次每支钢笔的进价是多少元?
(2)若要求这两次购进的钢笔按同一价格全部销售完毕后获利不低于350元,问每支售价至少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com