
【题目】如图,正方形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 的垂直平分线分别交
的垂直平分线分别交![]() ,
,![]() 及
及![]() 的延长线于点
的延长线于点![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,则下列结论中:①
,则下列结论中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤ ![]() ;⑥
;⑥![]() ;⑦
;⑦![]() .正确的结论的个数为( )
.正确的结论的个数为( )
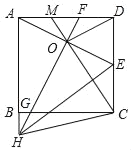
A.3B.4C.5D.6
【答案】B
【解析】
①作辅助线,构建三角形全等,证明△ADE≌△GKF,则FG=AE,可得FG=2AO;
②设正方形ABCD的边长为2x,则AD=AB=2x,DE=EC=x,证明△ADE∽△HOA,得![]() ,于是可求BH及HE的值,可作出判断;
,于是可求BH及HE的值,可作出判断;
③分别表示出OD、OC,根据勾股定理逆定理可以判断;
④证明∠HEA=∠AED=∠ODE,OE≠DE,则∠DOE≠∠HEA,OD与HE不平行;
⑤由②可得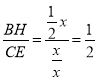 ,根据AR∥CD,得
,根据AR∥CD,得![]() ,则
,则![]() ;
;
⑥证明△HAE∽△ODE,可得![]() ,等量代换可得OE2=AHDE;
,等量代换可得OE2=AHDE;
⑦分别计算HC、OG、BH的长,可得结论.
解:①如图,过G作GK⊥AD于K,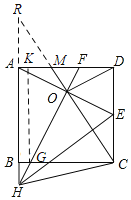
∴∠GKF=90°,
∵四边形ABCD是正方形,
∴∠ADE=90°,AD=AB=GK,
∴∠ADE=∠GKF,
∵AE⊥FH,
∴∠AOF=∠OAF+∠AFO=90°,
∵∠OAF+∠AED=90°,
∴∠AFO=∠AED,
∴△ADE≌△GKF,
∴FG=AE,
∵FH是AE的中垂线,
∴AE=2AO,
∴FG=2AO,
故①正确;
②设正方形ABCD的边长为2x,则AD=AB=2x,DE=EC=x,
![]() ,
,
易得△ADE∽△HOA,
![]()
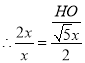 ,
,
![]() ,
,
Rt△AHO中,由勾股定理得:AH= 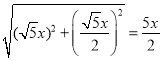 ,
,
∴BH=AH-AB= ![]() ,
,
∵HE=AH= ![]() ,
,
∴HE=5BH;
故②正确;
③![]() ,
,![]() ,
,![]()
∴![]() ,
,
∴OC与OD不垂直,
故③错误;
④∵FH是AE的中垂线,
∴AH=EH,
∴∠HAE=∠HEA,
∵AB∥CD,
∴∠HAE=∠AED,
Rt△ADE中,∵O是AE的中点,
∴OD=![]() AE=OE,
AE=OE,
∴∠ODE=∠AED,
∴∠HEA=∠AED=∠ODE,
当∠DOE=∠HEA时,OD∥HE,
但AE>AD,即AE>CD,
∴OE>DE,即∠DOE≠∠HEA,
∴OD与HE不平行,
故④不正确;
⑤由②知BH=![]() ,
,
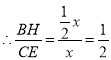 ,
,
延长CM、BA交于R,
∵RA∥CE,
∴∠ARO=∠ECO,
∵AO=EO,∠ROA=∠COE,
∴△ARO≌△ECO,
∴AR=CE,
∵AR∥CD,
![]() ,
,
![]()
![]()
故⑤正确;
⑥由①知:∠HAE=∠AEH=∠OED=∠ODE,
∴△HAE∽△ODE,
![]()
∵AE=2OE,OD=OE,
∴OE2OE=AHDE,
∴2OE2=AHDE,
故⑥正确;
⑦由②知:HC= 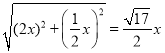 ,
,
∵AE=2AO=OH= ![]() ,
,
tan∠EAD= ![]() ,
,
![]() ,
,
![]() ,
,
∵FG=AE ![]() ,
,
![]() ,
,
∴OG+BH= ![]() ,
,
∴OG+BH≠HC,
故⑦不正确;
综上所述,本题正确的有;①②⑤⑥,共4个,
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,在某一路段,规定汽车限速行驶,交通警察在此限速路段的道路上设置了监测区,其中点C、D为监测点,已知点C、D、B在同一直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°
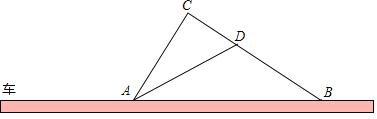
(1)求道路AB段的长(结果精确到1米)
(2)如果道路AB的限速为60千米/时,一辆汽车通过AB段的时间为90秒,请你判断该车是否是超速,并说明理由;参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002
查看答案和解析>>
科目:初中数学 来源: 题型:
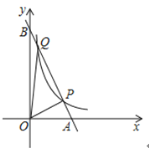
【题目】如图,已知反比例函数![]() 的图象与直线
的图象与直线![]() 都经过点
都经过点![]() ,
,![]() ,且直线
,且直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)直接写出![]() ,
,![]() 的值及直线
的值及直线![]() 的函数表达式;
的函数表达式;
(2)![]() 与
与![]() 的面积相等吗?写出你的判断,并说明理由;
的面积相等吗?写出你的判断,并说明理由;
(3)若点![]() 是
是![]() 轴上一点,当
轴上一点,当![]() 的值最小时,求点
的值最小时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有3,4,5,x,甲,乙两人每次同时从袋中各随机取出1个小球,并计算2个小球上的数字之和.记录后将小球放回袋中搅匀,进行重复试验,试验数据如下表:
摸球总 次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
“和为8”出 现的频数 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
“和为8”出 现的频率 | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
解答下列问题:
(1)如果试验继续进行下去,根据上表提供的数据,出现和为8的频率将稳定在它的概率附近,估计出现和为8的概率是________;
(2)如果摸出的2个小球上数字之和为9的概率是,那么x的值可以为7吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
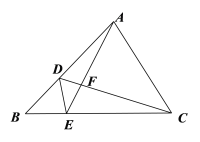
【题目】已知:如图,在△ABC中,点D,E分别在边AB,BC上,BABD=BCBE
(1)求证:△BDE∽△BCA;
(2)如果AE=AC,求证:AC2=ADAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料1:如图1,昌平南环大桥是经典的悬索桥,当今大跨度桥梁大多采用此种结构.此种桥梁各结构的名称如图2所示,其建造原理是在两边高大的桥塔之间,悬挂着主索,再以相应的间隔,从主索上设置竖直的吊索,与桥面垂直,并连接桥面承接桥面的重量,主索几何形态近似符合抛物线.

图1
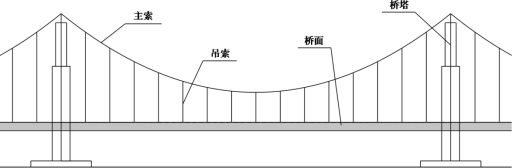
图2
材料2:如图3,某一同类型悬索桥,两桥塔AD=BC=10 m,间距AB为32 m,桥面AB水平,主索最低点为点P,点P距离桥面为2 m;

图3
为了进行研究,甲、乙、丙三位同学分别以不同方式建立了平面直角坐标系,如下图:
甲同学:以DC中点为原点,DC所在直线为x轴,建立平面直角坐标系;

乙同学:以AB中点为原点,AB所在直线为x轴,建立平面直角坐标系;

丙同学:以点P为原点,平行于AB的直线为x轴,建立平面直角坐标系.
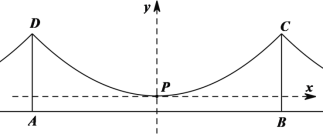
(1)请你选用其中一位同学建立的平面直角坐标系,写出此种情况下点C的坐标,并求出主索抛物线的表达式;
(2)距离点P水平距离为4 m和8 m处的吊索共四条需要更换,则四根吊索总长度为多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com