
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:解答题
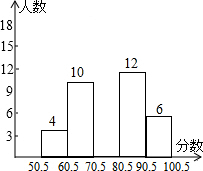 某班数学期末考试后,班主任将所得的成绩(分数取整数)进行整理分成5组,并绘成频数分布直方图(如图),已知70.5~80.5分数段的频率为0.36,请结合直方图提供的信息,解答以下问题:
某班数学期末考试后,班主任将所得的成绩(分数取整数)进行整理分成5组,并绘成频数分布直方图(如图),已知70.5~80.5分数段的频率为0.36,请结合直方图提供的信息,解答以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一、三 | B. | 二、四 | C. | 三、四 | D. | 一、二 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 金额(元) | 20 | 30 | 35 | 50 | 100 |
| 学生数(人) | 10 | 13 | 5 | 15 | 2 |
| A. | 15,13 | B. | 15,30 | C. | 50,30 | D. | 50,35 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
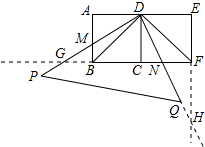 如图,两个边长均为2的正方形ABCD和正方形CDEF,点B、C、F在同一直线上,一直角三角板(即Rt△PDQ)的直角顶点放置在点D处,DP交AB于点M,DQ交BF于点N.
如图,两个边长均为2的正方形ABCD和正方形CDEF,点B、C、F在同一直线上,一直角三角板(即Rt△PDQ)的直角顶点放置在点D处,DP交AB于点M,DQ交BF于点N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com