
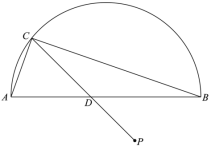
����Ŀ������ƽ��ֱ������ϵxOy�еĶ���P��ͼ��F���������¶��壺����ͼ��F�ϴ���һ��N��ʹ�õ�Q����P����ֱ��ON�Գƣ���Ƶ�Q�ǵ�P����ͼ��F�Ķ���ԳƵ㣮
��1����ͼ��![]() ��
��![]() ��
��![]() ��
��

����P���ڵ�B�Ķ���ԳƵ�������� ��
���ڵ�![]() ��
��![]() ��
��![]() �У�______�ǵ�P�����߶�AB�Ķ���ԳƵ㣮
�У�______�ǵ�P�����߶�AB�Ķ���ԳƵ㣮
��2��ֱ��![]() �ֱ���x�ᣬy�ύ�ڵ�G��H����M���Ե�
�ֱ���x�ᣬy�ύ�ڵ�G��H����M���Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��Բ��
Ϊ�뾶��Բ��
����![]() ʱ������M�ϴ��ڵ�K��ʹ���������߶�GH�Ķ���ԳƵ����߶�GH�ϣ���
ʱ������M�ϴ��ڵ�K��ʹ���������߶�GH�Ķ���ԳƵ����߶�GH�ϣ���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
������![]() ����
����![]() ʱ�����߶�GH�ϴ��ڵ�J��ʹ����������M�Ķ���ԳƵ�����M�ϣ�ֱ��д��b��ȡֵ��Χ��
ʱ�����߶�GH�ϴ��ڵ�J��ʹ����������M�Ķ���ԳƵ�����M�ϣ�ֱ��д��b��ȡֵ��Χ��
���𰸡���1����![]() ������C��D����2����
������C��D����2����![]() ��
��![]() ����
����![]() ��
��
��������
��1���������P����ֱ��OB�ĶԳƵ�G���ɣ�
�����OP��OC��OD��OE�ij������жϣ�
��2���������������λ��b��ֵ���ɣ���ͼ2�У�����M����y��ĶԳ�ͼ����M�䣬��ֱ��GH����M���ڵ�һ��������ʱ�����е�ΪP������PM�䣮��ͼ3�У���OΪԲ�ģ�3Ϊ�뾶����O����ֱ��GH����O�ڵ������������ڵ�Pʱ������OP���ֱ����OH��ֵ���ɽ�����⣮
����ͼ4�У�����M��x����K��T����K����1��0����T��5��0���������������λ��b��ֵ�����жϣ�
�⣺��1������ͼ1�У�
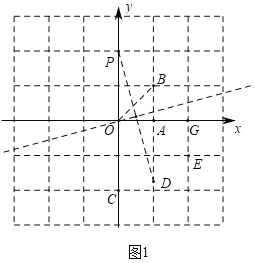
��P��0��2����B��1��1����
���P����OB�ĶԳƵ�G��2��0����
�ʴ�Ϊ����2��0����
���ߵ�C��0����2����D��1����![]() ����E��2����1����
����E��2����1����
��OP��2��OD��2��OC��2��OE��![]() ��
��
��OP��OD��OC��
���C��D�ǵ�P�����߶�AB�Ķ���ԳƵ㣮
�ʴ�Ϊ����C��D��
��2������ͼ2�У�����M����y��ĶԳ�ͼ����M�䣬��ֱ��GH����M���ڵ�һ��������ʱ�����е�ΪP������PM�䣬
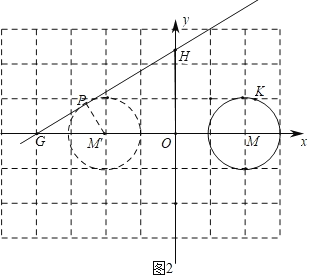
��b��0ʱ��
������ã�tan��HGO��![]() ��
��
���PGM��30�㣬
��PM�䣽1����MPG��90�㣬
��MG��2MP��2��
��OG��GM+OM��4��
��OH��OGtan30�㣽![]() ��
��
��ֱ�߾�����-1��0��ʱ��![]() .
.
��![]()
��b��0ʱ��
����ֱ�߾�����1��0��ʱ��![]() .
.
��ͼ3�У���OΪԲ�ģ�3Ϊ�뾶����O����ֱ��GH����O�ڵ������������ڵ�Pʱ������OP��
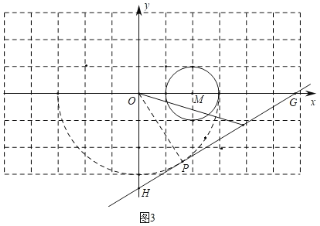
ͬ���ɵ�OH��2![]() ����
����![]()
�۲�ͼ���֪����������b��ֵ����2![]() ��b��
��b��![]() ��
��
����������b��ȡֵ��Χ��![]() ��
��![]() .
.
����ͼ4�У�����M��x����K��T����K����1��0����T��5��0����
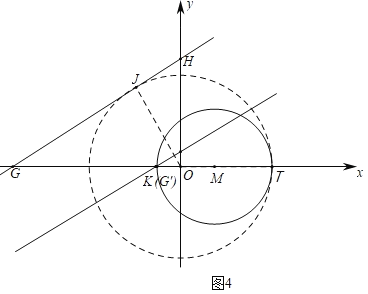
��OΪԲ�ģ�5Ϊ�뾶����O����ֱ��GH����O�ڵڶ����������ڵ�Jʱ��
�ɵ�OH�� ��
��
��ʱֱ��GH�Ľ���ʽΪy��![]() x+
x+![]() ��
��
��ֱ��GH������K����1��0��ʱ��0����![]() +b��
+b��
�ɵ�b��![]() ��
��
��ʱֱ��GH�Ľ���ʽΪy��![]() x+
x+![]() ��
��
�۲�ͼ���֪����������b��ֵΪ��![]() ��b��
��b��![]() ��
��


 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �ǰ�Բ��ֱ����P�ǰ�Բ��ֱ��
�ǰ�Բ��ֱ����P�ǰ�Բ��ֱ��![]() ��Χ�ɵ�ͼ�ε��ⲿ��һ���㣬D��ֱ��
��Χ�ɵ�ͼ�ε��ⲿ��һ���㣬D��ֱ��![]() ��һ���㣬����
��һ���㣬����![]() ���ӳ�������Բ�ڵ�C������
���ӳ�������Բ�ڵ�C������![]() ����֪
����֪![]() ����
����![]() �����ľ���Ϊ
�����ľ���Ϊ![]() ��
��![]() ����֮��ľ���Ϊ
����֮��ľ���Ϊ![]() ����֮��ľ���Ϊ
����֮��ľ���Ϊ![]() ��
��
С������ѧϰ�����ľ��飬�ֱ�Ժ���![]() ���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����
���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����
������С����̽�����̣��벹��������
��1�������±��Ա���x��ֵ����ȡ�㡢��ͼ���������ֱ�õ�![]() ��x�ļ����Ӧֵ��
��x�ļ����Ӧֵ��
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0.47 | 1.31 | 5.02 | 5.91 | 6 | |
| 6 | 5.98 | 5.86 | 5.26 | 3.29 | 1.06 | 0 |
��2����ͬһƽ��ֱ������ϵ![]() �У������ȫ��ı��и�����ֵ����Ӧ�ĵ�
�У������ȫ��ı��и�����ֵ����Ӧ�ĵ�![]() ��
��![]() ������������
������������![]() ��ͼ��
��ͼ��
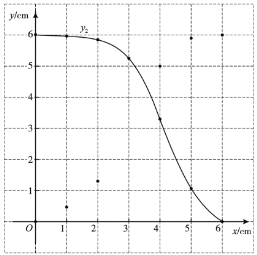
��3����Ϻ���ͼ������⣺��![]() ��һ���ǵ�����ֵΪ
��һ���ǵ�����ֵΪ![]() ʱ��
ʱ��![]() �ij�ԼΪ_____cm��
�ij�ԼΪ_____cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ƶ������Ϊһƶ�����ṩ��![]() ��Ԫ����Ϣ��ƶ�����ƶ����������ʴ��ע����һ�����꣬����һ�ֳɱ���Ϊ
��Ԫ����Ϣ��ƶ�����ƶ����������ʴ��ע����һ�����꣬����һ�ֳɱ���Ϊ![]() Ԫ/����ũ��Ʒ����֪���ۼ۸��ڳɱ��ۣ��Ҳ�����
Ԫ/����ũ��Ʒ����֪���ۼ۸��ڳɱ��ۣ��Ҳ�����![]() Ԫ/��������ÿ����֧����ѵ���������
Ԫ/��������ÿ����֧����ѵ���������![]() ǧԪ�г����鷢�֣���ũ��Ʒÿ��������Ϊ
ǧԪ�г����鷢�֣���ũ��Ʒÿ��������Ϊ![]() (�ټ�)�����ۼ�
(�ټ�)�����ۼ�![]() (Ԫ/��)֮��ĺ�����ϵ��ͼ��ʾ
(Ԫ/��)֮��ĺ�����ϵ��ͼ��ʾ
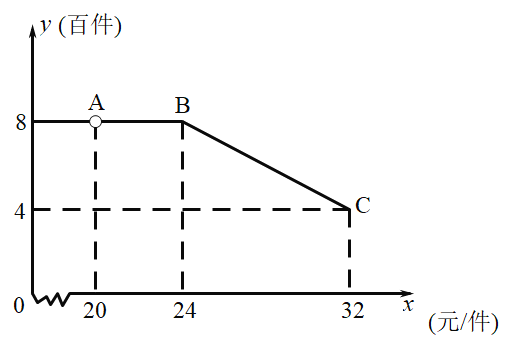
��1���������ÿ������![]() (��Ԫ)�����ۼ�
(��Ԫ)�����ۼ�![]() (Ԫ/��)֮��ĺ�����ϵʽ����ע���Ա���
(Ԫ/��)֮��ĺ�����ϵʽ����ע���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����ƶ���������꿪ҵ������ڵڼ����¿���������������Ϣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() ��ĸ����ύ�ڵ�
��ĸ����ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ������
������![]() ����C(6��
����C(6��![]() )���������ϣ�ֱ��
)���������ϣ�ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]()
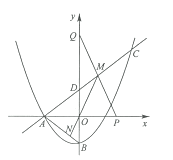
(1)��![]() ��ֵ��ֱ��
��ֵ��ֱ��![]() �ĺ�������ʽ��
�ĺ�������ʽ��
(2)��![]() ��
��![]() ���������ϣ���
���������ϣ���![]() ��
��![]() ���������ϣ�����
���������ϣ�����![]() ��ֱ��
��ֱ��![]() ���ڵ�
���ڵ�![]() ������
������![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() ����
����![]() Ϊ
Ϊ![]() ���е㣮
���е㣮
����֤��![]() ��
��
�����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ����
����![]() �ij�(�ú�
�ij�(�ú�![]() �Ĵ���ʽ��ʾ)��
�Ĵ���ʽ��ʾ)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����C��D�ǡ�O�����㣬��![]() ������OC��BD��OD��
������OC��BD��OD��
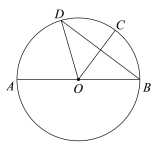
��1����֤��OC��ֱƽ��BD��
��2������C����O�����߽�AB���ӳ����ڵ�E������AD��CD��
�������ⲹȫͼ�Σ�
����AD=6��![]() ����CD�ij���
����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB = 90��DΪAB���е㣬AE��DC��CE��DA��
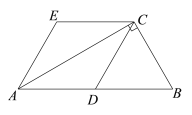
��1����֤���ı���ADCE�����Σ�
��2������DE����AC =![]() ��BC =2����֤����ADE�ǵȱ������Σ�
��BC =2����֤����ADE�ǵȱ������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵxOy�еĶ���P��ͼ��F���������¶��壺����ͼ��F�ϴ���һ��N��ʹ�õ�Q����P����ֱ��ON�Գƣ���Ƶ�Q�ǵ�P����ͼ��F�Ķ���ԳƵ㣮
��1����ͼ��![]() ��
��![]() ��
��![]() ��
��

����P���ڵ�B�Ķ���ԳƵ�������� ��
���ڵ�![]() ��
��![]() ��
��![]() �У�______�ǵ�P�����߶�AB�Ķ���ԳƵ㣮
�У�______�ǵ�P�����߶�AB�Ķ���ԳƵ㣮
��2��ֱ��![]() �ֱ���x�ᣬy�ύ�ڵ�G��H����M���Ե�
�ֱ���x�ᣬy�ύ�ڵ�G��H����M���Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��Բ��
Ϊ�뾶��Բ��
����![]() ʱ������M�ϴ��ڵ�K��ʹ���������߶�GH�Ķ���ԳƵ����߶�GH�ϣ���
ʱ������M�ϴ��ڵ�K��ʹ���������߶�GH�Ķ���ԳƵ����߶�GH�ϣ���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
������![]() ����
����![]() ʱ�����߶�GH�ϴ��ڵ�J��ʹ����������M�Ķ���ԳƵ�����M�ϣ�ֱ��д��b��ȡֵ��Χ��
ʱ�����߶�GH�ϴ��ڵ�J��ʹ����������M�Ķ���ԳƵ�����M�ϣ�ֱ��д��b��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����̳�����ÿ̨���۷ֱ�Ϊ200Ԫ��170Ԫ��A��B�����ͺŵĵ���ȣ��±��Ǹ��ͺŵ���Ƚ����ܵ����������
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 3̨ | 5̨ | 1800Ԫ |
�ڶ��� | 4̨ | 10̨ | 3100Ԫ |
![]() ��A��B�����ͺŵĵ���ȵ����۵��ۣ�
��A��B�����ͺŵĵ���ȵ����۵��ۣ�
![]() �����̳����ò�����5400Ԫ�Ľ���ٲɹ��������ͺŵĵ���ȹ�30̨�������ۼ۲��䣬��ô�̳�Ӧ�������ֲɹ�����������ʹ�õ���������Щ���Ⱥ��̳�������ࣿ���ɻ�������Ԫ��
�����̳����ò�����5400Ԫ�Ľ���ٲɹ��������ͺŵĵ���ȹ�30̨�������ۼ۲��䣬��ô�̳�Ӧ�������ֲɹ�����������ʹ�õ���������Щ���Ⱥ��̳�������ࣿ���ɻ�������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�߳�Ϊ5������ABCD�У��Խ���AC��Ϊ6����E�ڶԽ���BD����tan��EAC=![]() ����BE�ij�Ϊ_____��
����BE�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com