
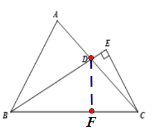
【题目】如图,在△ABC中, BD是∠ABC的平分线,过点C作CE⊥BD,交 BD的延长线于点E,∠ABC=60°,∠ECD=15°.
(1)直接写出∠ADB的度数是_______;
(2)求证:BD=AB;
(3)若AB=2,求BC的长.

【答案】(1)75°;(2)证明见解析;(3)BC=![]() .
.
【解析】
(1)先求出∠EDC的度数,从而求出∠EDC的对顶角∠ADB;
(2)根据条件求出∠ADB=75°,得出∠A=75°,随之即可解答.
(3)过点D作DF⊥BC,交BC于F点,根据条件求出FB,FC的长度即可解答.
(1)75°
∠EDC=90°-∠ECD=75°,∴∠ADB=∠EDC=75°.
(2)证明:∵BD平分∠ABC
∠ABC=60°
∴∠ABD=∠DBC=30°
∵∠ADB=75°
∴∠A=75°
∴∠A=∠ADB
∴AB=DB
(3)过点D作DF⊥BC,交BC于F点
∵DF⊥BC
∴∠DFB=∠DFC=90°
∵∠DBF=30°
∴DF=![]() BD
BD
∵BD=AB=2
∴DF =1
∴FB=![]()
∵CE⊥BE
∴∠E=90°
∵∠DBC=30°
∴∠ECB=60°
∵∠ECD=15°
∴∠DCB=45°
∴∠DCF=∠FDC=45°
∴FC= FD=1
∴BC=![]()


科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+6交x轴于A,交y轴于B.

(1)直接写出A( , ),B( , );
(2)如图1,点E为直线y=x+2上一点,点F为直线y=![]() x上一点,若以A,B,E,F为顶点的四边形是平行四边形,求点E,F的坐标
x上一点,若以A,B,E,F为顶点的四边形是平行四边形,求点E,F的坐标
(3)如图2,点C(m,n)为线段AB上一动点,D(﹣7m,0)在x轴上,连接CD,点M为CD的中点,求点M的纵坐标y和横坐标x之间的函数关系式,并直接写出在点C移动过程中点M的运动路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y= ![]() x-3与反比例函数y=
x-3与反比例函数y= ![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.
(1)填空:n的值为 , k的值为;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数y= ![]() 的图象,当y≥-2时,请直接写出自变量x的取值范围.
的图象,当y≥-2时,请直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市创全国卫生城市,某街道积极响应,决定在街道内的所有小区安装垃圾分类的温馨提示牌和垃圾箱,若购买4个垃圾箱比购买5个温馨提示牌多350元,垃圾箱的单价是温馨提示牌单价的3倍.
![]() 求温馨提示牌和垃圾箱的单价各是多少元?
求温馨提示牌和垃圾箱的单价各是多少元?
![]() 如果该街道需购买温馨提示牌和垃圾箱共3000个.
如果该街道需购买温馨提示牌和垃圾箱共3000个.
![]() 求购买温馨提示牌和垃圾箱所需费用
求购买温馨提示牌和垃圾箱所需费用![]() 元
元![]() 与温馨提示牌的个数x的函数关系式;
与温馨提示牌的个数x的函数关系式;
![]() 若该街道计划费用不超过35万元,而且垃圾箱的个数不少于温馨提示牌的个数的
若该街道计划费用不超过35万元,而且垃圾箱的个数不少于温馨提示牌的个数的![]() 倍,求有几种可供选择的方案?并找出资金最少的方案,求出最少需多少元?
倍,求有几种可供选择的方案?并找出资金最少的方案,求出最少需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M为正方形ABCD边AB的中点,E是AB延长线上的一点,MN⊥DM,且交∠CBE的平分线于N.
(1)求证:MD=MN;
(2)若将上述条件中的“M为AB边的中点”改为“M为AB边上任意一点”,其余条件不变,则结论“MD=MN”成立吗?如果成立,请证明;如果不成立,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛,各参赛选手的成绩如下(单位:分):
A班:88,91,92,93,93,93,94,98,98,100
B班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
A班 | 100 | a | 93 | 93 | c |
B班 | 99 | 95 | b | 93 | 8.4 |
(1)求表中a、b、c的值;
(2)依据数据分析表,有人说:“最高分在A班,A班的成绩比B班好”,但也有人说B班的成绩要好,请给出两条支持B班成绩好的理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于点Q。
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向点D运动(不与点D重合),设点P运动时间为t秒,请用t表示PD的长;并求当t为何值时,四边形PBQD是菱形。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com