【题目】如图，△ABC中，∠C=70°，⊙O切CA、CB分别于点A和点B，则弦AB所对的圆周角的度数为（ ）
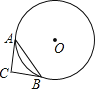
A. 110° B. 55° C. 55°或 110° D. 55 或 125°
【答案】D
【解析】
由CA、CB是⊙O的切线，∠C=70°，根据切线的性质，易求得∠AOB的度数，然后由圆周角定理，可求得当点D在优弧AB上时，∠ADB的值，由圆的内接四边形的性质，可求得当点E在劣弧AB上时，∠AEB的度数，继而求得答案．
连接OA、OB，
∵CA、CB是⊙O的切线，
∴OA⊥CA，OB⊥CB，
∴∠CAO=∠CBO=90°，
∵∠C=70°，
∴∠AOB=360°-∠CAO-∠CBO-∠C=110°，
∴当点D在优弧AB上时，∠ADB=
∠AOB=55°；
当点E在劣弧AB上时，∠AEB=180°-∠ADB=125°．
∴弦AB所对的圆周角的度数是：55°或125°．
故选D．
科目：初中数学 来源： 题型：
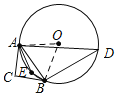
【题目】如图，直线
与⊙
相切于点
为⊙的直径， 
是直径
右侧半圆上的一个动点(不与点
、
重合)，过点
作
，垂足为
，连接
、
.设
, 
.求: (1)
与
相似吗?为什么?
(2)求
与
的函数关系式;
(3)当为何值时，
取得最大值，最大值为多少?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】投资1万元围一个矩形菜园(如图)，其中一边靠墙，另外三边选用不同材料建造.墙长24 m，平行于墙的边的费用为200元/m，垂直于墙的边的费用为150元/m，设平行于墙的边长为x m.
(1)设垂直于墙的一边长为y m，直接写出y与x之间的函数关系式；
(2)若菜园面积为384 m2，求x的值；
(3)求菜园的最大面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
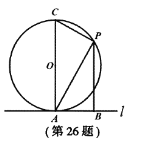
【题目】如图，两条公路
、
交予点
，在公路旁有一学校
，与点的距离为
，点（学校）到公路的距离
为
．一大货车从点出发，行驶在公路上，汽车周围
范围内有噪音影响．
（1）货车开过学校是否受噪音影响？为什么？
（2）若汽车速度为
，则学校受噪音影响多少秒钟？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知AB是⊙O的直径，AB=4，点C，点D在⊙O上，CD=2，直线AD，BC交于点E．
(1)如图，若点E在⊙O外，求∠AEB的度数．
(2)若DC∥AB，试求出△ABE的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD的对角线AC与BD相交于点O，∠ACB的平分线分别交AB、BD于M、N两点．若AM=
，则线段BN的长为（ ）
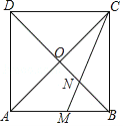
A.1B.C.2D.
查看答案和解析>>
科目：初中数学 来源： 题型：
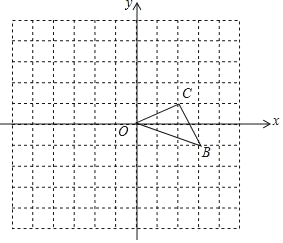
【题目】如图，在平面直角坐标系中，点B的坐标为（3，﹣1）．
(1)以点O为位似中心，在y轴的左侧将△OBC放大到原来的两倍（即新图与原图的相似比为2），画出放大后的△OB′C′；
(2)在(1)的基础上写出点B′，C′的坐标；
(3)在(1)的基础上，如果△OBC内部一点M的坐标为（a，b），请写出M的对应点M′的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
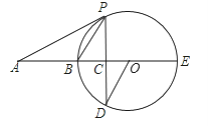
【题目】如图，BE是圆O的直径，A在EB的延长线上，AP为圆O的切线，P为切点，弦PD垂直于BE于点C．
（1）求证：∠AOD=∠APC；
（2）若OC：CB=1：2，AB=6，求圆O的半径及tan∠APB．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
