
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

科目:初中数学 来源: 题型:
【题目】某体育用品制造公司通过互联网销售某品牌排球,第一周的总销售额为3000元,第二周的总销售额为3520元,第二周比第一周多售出13个排球.
(1)求每个排球的售价;
(2)该公司在第三周将每个排球的售价降低了![]() (其中
(其中![]() ),并预计第三周能售出120个排球.恰逢中国女排夺冠,极大地激发了广大青少年积极参与排球运动的热情,该款排球在第三周的销量比预计的120个还多了
),并预计第三周能售出120个排球.恰逢中国女排夺冠,极大地激发了广大青少年积极参与排球运动的热情,该款排球在第三周的销量比预计的120个还多了![]() .已知每个排球的成本为16元,该公司第三周销售排球的总利润为4320元,求
.已知每个排球的成本为16元,该公司第三周销售排球的总利润为4320元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场设立了一个可以自由转动的转盘,并做如下规定:顾客购物80元以上就获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据.

(1)计算并完成表格;
(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动该盘一次,你获得洗衣粉的概率约是多少?
(4)在该转盘中,表示“洗衣粉”区域的扇形的圆心角约是多少?(精确到1°)
查看答案和解析>>
科目:初中数学 来源: 题型:
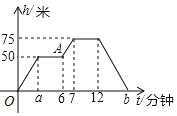
【题目】某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是______,因变量是______;
(2)无人机在75米高的上空停留的时间是______分钟;
(3)在上升或下降过程中,无人机的速度______为米/分;
(4)图中a表示的数是______;b表示的数是______;
(5)图中点A表示______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是推导“三角形内角和定理”的学习过程,请补全证明过程及推理依据.

已知:如图,△ABC.
求证:∠A+∠B+∠C=180°.
证明:过点A作DE∥BC,(请在图上画出该辅助线并标注D,E两个字母)
∠B=∠BAD,∠C= .( )
∵点D,A,E在同一条直线上,
∴ (平角的定义)
∴∠B+∠BAC+∠C=180°
即三角形的内角和为180°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3cm/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单 位:s)(0<t<![]() )。
)。
(1)如图1,连接DQ平分∠BDC时,t的值为 ;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O始终在QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com