
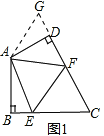
【题目】(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段EF,BE,FD之间的数量关系.
小明同学探究的方法是:延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,
他的结论是 (直接写结论,不需证明);
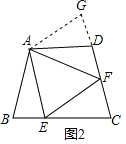
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC,CD上的点,且∠EAF是∠BAD的二分之一,上述结论是否仍然成立,并说明理由.
(3)如图3,四边形ABCD是边长为5的正方形,∠EBF=45°,直接写出三角形DEF的周长.

【答案】(1)EF=BE+DF.(2)成立,理由见解析;(3)10.
【解析】
(1)如图1,延长FD到G,使得DG=DC,先证△ABE≌△ADG,得到AE=AG,∠BAE=∠DAG,进一步根据题意得∠EAF=∠GAF,再证明△AEF≌△AGF,得到EF=FG,最后运用线段的和差证明即可.
(2) 如图2,延长FD到点G.使DG=BE.连结AG,证得△ABE≌△ADG,得到AE=AG,∠BAE=∠DAG,再结合题意得到∠EAF=∠GAF,再证明△AEF≌△AGF,得到EF=FG,最后运用线段的和差证明即可.
(3)如图3,延长DC到点G,截取CG=AE,连接BG,先证△AEB≌△CGB,得到BE=BG,∠ABE=∠CBG,结合已知条件得∴∠CBF+∠CBG=45°,再证明△EBF≌△GBF,得到EF=FG,最后求三角形的周长即可.
解答:(1)解:如图1,延长FD到G,使得DG=DC
在△ABE和△ADG中,
∵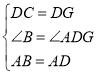
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
∵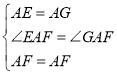 ,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
故答案为:EF=BE+DF.
(2)解:结论EF=BE+DF仍然成立;
理由:如图2,延长FD到点G.使DG=BE.连结AG
在△ABE和△ADG中,
∵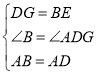 ,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
∵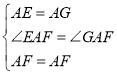 ,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
(3)解:如图3,延长DC到点G,截取CG=AE,连接BG,
在△AEB与△CGB中,
∵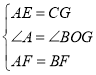
,
∴△AEB≌△CGB(SAS),
∴BE=BG,∠ABE=∠CBG.
∵∠EBF=45°,∠ABC=90°,
∴∠ABE+∠CBF=45°,
∴∠CBF+∠CBG=45°.
在△EBF与△GBF中,
∵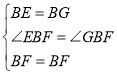 ,
,
∴△EBF≌△GBF(SAS),
∴EF=GF,
∴△DEF的周长=EF+ED+CF=AE+CF+DE+DF=AD+CD=10.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是( ).
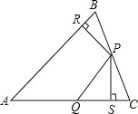
A.①②B.①②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在探索三角形全等的条件时,老师给出了定长线段![]() ,且长度为
,且长度为![]() 的边所对的角为
的边所对的角为![]() 小明和小亮按照所给条件分别画出了图1中的三角形,他们把两个三角形重合在一起(如图2),其中
小明和小亮按照所给条件分别画出了图1中的三角形,他们把两个三角形重合在一起(如图2),其中![]() 发现它们不全等,但他们对该图形产生了浓厚兴趣,并进行了进一步的探究:
发现它们不全等,但他们对该图形产生了浓厚兴趣,并进行了进一步的探究:


(1)当![]() 时(如图2),小明测得
时(如图2),小明测得![]() ,请根据小明的测量结果,求
,请根据小明的测量结果,求![]() 的大小;
的大小;
(2)当![]() 时,将
时,将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() (如图3),小明和小亮发现
(如图3),小明和小亮发现![]() 的大小与角度
的大小与角度![]() 有关,请找出它们的关系,并说明理由;
有关,请找出它们的关系,并说明理由;
(3)如图4,在(2)问的基础上,过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,延长
,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,请判断
,请判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
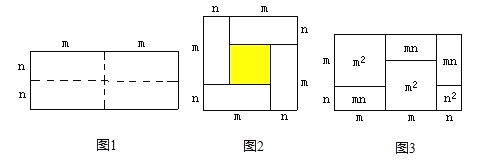
【题目】如图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)图2中间的小正方形(即阴影部分)面积可表示为________________.
(2)观察图2,请你写出三个代数式(m+n)2,(m-n)2,mn之间的等量关系式:______________.
(3)根据(2)中的结论,若x+y=-6,xy=2.75,则x-y=____________.
(4)有许多代数恒等式可以用图形的面积来表示.如图3所示,它表示了(2m+n)(m+n)=2m2+3mn+n2.试画出一个几何图形,使它的面积能表示为(m+n)(m+2n)=m2+3mn+2n2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图①,在直角三角形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,可知
,可知![]() (不需要证明);
(不需要证明);
(1)探究:如图②,![]() ,射线
,射线![]() 在这个角的内部,点
在这个角的内部,点![]() 、
、![]() 在
在![]() 的边
的边![]() 、
、![]() 上,且
上,且![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .证明:
.证明:![]() ;
;
(2)证明:如图③,点![]() 、
、![]() 在
在![]() 的边
的边![]() 、
、![]() 上,点
上,点![]() 、
、![]() 在
在![]() 内部的射线
内部的射线![]() 上,
上,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的外角。已知
的外角。已知![]() ,
,![]() .求证:
.求证:![]() ;
;
(3)应用:如图④,在![]() 中,
中,![]() ,
,![]() .点
.点![]() 在边
在边![]() 上,
上,![]() ,点
,点![]() 、
、![]() 在线段
在线段![]() 上,
上,![]() .若
.若![]() 的面积为15,则
的面积为15,则![]() 与
与![]() 的面积之和为________.
的面积之和为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() (k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(1)求这个反比函数的表达式;
(2)求△ACD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com