
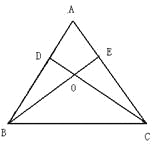
【题目】已知:如图,锐角△ABC的两条高BE、CD相交于点O,且OB=OC,
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由。
【答案】(1)、证明过程见解析;(2)、点O是在∠BAC的角平分线上,理由见解析.
【解析】试题分析:(1)、根据等腰三角形的性质以及高线得出△BDC和△CEB全等,从而得出∠DBC=∠ECB,得到等腰三角形;(2)、连接AO,根据△BDC和△CEB全等得到DC=EB,然后根据OB=OC得出OD=OE,结合∠BDC=∠CEB=90°和AO为公共边得出△ADO和△AEO全等从而得到答案.
试题解析:(1)、∵OB=OC ∴∠OBC=∠OCB ∵BE、CD是两条高 ∴∠BDC=∠CEB=90°
又∵BC=CB ∴△BDC≌△CEB(AAS) ∴∠DBC=∠ECB ∴AB=AC ∴△ABC是等腰三角形。
(2)、点O是在∠BAC的角平分线上。连结AO. ∵ △BDC≌△CEB ∴DC=EB,
∵OB=OC ∴ OD=OE 又∵∠BDC=∠CEB=90° AO=AO ∴△ADO≌△AEO(HL)
∴∠DAO=∠EAO ∴点O是在∠BAC的角平分线上。



科目:初中数学 来源: 题型:
【题目】阅读下面的对话。
小红:“售货员,我要买些梨。”
售货员说:“小红,你上次买的那种梨卖完了,我们还没来得及进货,我建议你这次买些新进的苹果,价格比梨贵一点,不过这批苹果的味道挺好哟!”
小红:“好,这次和上次一样,也花30元。”
对照前后两次的电脑小票,小红发现,每千克苹果的单价是梨的1.5倍,买的苹果的重量比梨轻2.5Kg。
试根据上面的对话和小红的发现,分别求出苹果和梨的单价。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (
(![]() )与y轴交于点A,与x轴交于B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4,现将抛物线沿BA方向平移,平移后的抛物线过点C时,与x轴的另一点为E,其顶点为F,对称轴与x轴的交点为H.
)与y轴交于点A,与x轴交于B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4,现将抛物线沿BA方向平移,平移后的抛物线过点C时,与x轴的另一点为E,其顶点为F,对称轴与x轴的交点为H.
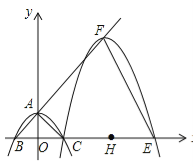
(1)求a、c的值及抛物线的解析式.
(2)连接OF,试判断△OEF是否为等腰三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知坐标平面内的三个点A(1,3),B(3,1),O(0,0),把△ABO向下平移3个单位再向右平2个单位后得△DEF.

(1)直接写出A、B、O三个对应点D、E、F的坐标;
(2)求△DEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com