

分析 (1)根据正弦的定义求出AE的最小值;
(2)过F作FM⊥EC交EC延长线于M,设BE=CF=2a,根据正弦、余弦的定义求出FM、CM,根据勾股定理列出算式,整理得到二次函数解析式,根据二次函数的性质计算即可;
(3)建立坐标系,根据待定系数法求出CD的解析式,得到线段CD的垂直平分线的解析式,根据勾股定理计算即可.
解答 解:(1)当AE⊥BC时,AE最小,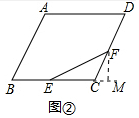
AE=AB×sinB=3$\sqrt{3}$,
即AE的最小值为3$\sqrt{3}$;
(2)过F作FM⊥EC交EC延长线于M,
设BE=CF=2a,则EC=6-a
CM=FC×cos∠FCM=a,FM=FC×sin∠FCM=$\sqrt{3}$a,
∴EF2=(6-2a+a)2+($\sqrt{3}$a)2=4a2-12a+36=4(x-$\frac{3}{2}$)2+27,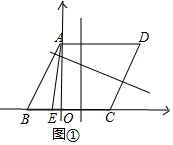
∴EF的最小值为$\sqrt{27}$=3$\sqrt{3}$;
(3)建立如图①所示坐标系.
则AO=3$\sqrt{3}$,
∵tan∠AEC=3$\sqrt{3}$,
∴OE=1,EC=OE+OC=1+3=4,
点C(3,0),D(6,3$\sqrt{3}$),A(0,3$\sqrt{3}$),
设直线CD的解析式为y=kx+b,
则$\left\{\begin{array}{l}{3k+b=0}\\{6k+b=3\sqrt{3}}\end{array}\right.$,
解得,k=$\sqrt{3}$,b=-3$\sqrt{3}$,
∴直线CD的解析式为:y=$\sqrt{3}$x-3$\sqrt{3}$,
则线段CD的垂直平分线的解析式为:y=-$\frac{\sqrt{3}}{3}$+3$\sqrt{3}$,
线段EC的垂直平分线为:x=1,
当x=1时,y=$\frac{8}{3}$$\sqrt{3}$,
∴到E点,C点、D点的距离相等的点的坐标为(1,$\frac{8}{3}$$\sqrt{3}$),
这个距离为:$\sqrt{{2}^{2}+(\frac{8}{3}\sqrt{3})^{2}}$=$\frac{{2\sqrt{57}}}{3}$.
点评 本题考查的是菱形的性质、二次函数的图象和性质、勾股定理的应用,掌握菱形的性质定理、正确得到二次函数的解析式、掌握二次函数的性质是解题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
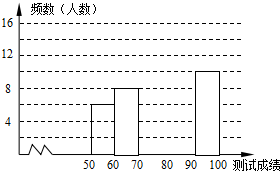 “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 6 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 14 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
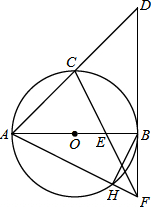 如图,AB是⊙O的直径,C是AD的中点,⊙O的切线BD交AC的延长线于点D,E是OB上一点,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.
如图,AB是⊙O的直径,C是AD的中点,⊙O的切线BD交AC的延长线于点D,E是OB上一点,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某公路圆弧弯道半径OA为1.5km,弯道两端A,B的直线距离为2km,求:
如图,某公路圆弧弯道半径OA为1.5km,弯道两端A,B的直线距离为2km,求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com