
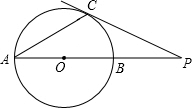
 如图,已知⊙O的直径AB与弦AC的夹角为30°,过C点的切线PC与AB的延长线于P.若圆半径等于5,则线段CP的长度是( )
如图,已知⊙O的直径AB与弦AC的夹角为30°,过C点的切线PC与AB的延长线于P.若圆半径等于5,则线段CP的长度是( )| A. | 5$\sqrt{3}$ | B. | 5 | C. | 10 | D. | $\frac{5\sqrt{3}}{3}$ |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某乡镇准备在相距3千米的A、B两个工厂间修建一条笔直的公路,在工厂A北偏东60°方向,工厂北偏西45°方向有一点P,以P点为圆心,1.2千米为半径的区域是一个村庄,问修筑公路时,这个村庄是否有居民需要搬迁?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
某乡镇准备在相距3千米的A、B两个工厂间修建一条笔直的公路,在工厂A北偏东60°方向,工厂北偏西45°方向有一点P,以P点为圆心,1.2千米为半径的区域是一个村庄,问修筑公路时,这个村庄是否有居民需要搬迁?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-3)^{2}}$=-3 | B. | a2+a4=a6 | C. | (-$\frac{1}{3}$)-1=$\frac{1}{3}$ | D. | (-π)0=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| h | 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com