
【题目】(2017宁夏)在边长为2的等边三角形ABC中,P是BC边上任意一点,过点 P分别作 PM⊥A B,PN⊥AC,M、N分别为垂足.
(1)求证:不论点P在BC边的何处时都有PM+PN的长恰好等于三角形ABC一边上的高;
(2)当BP的长为何值时,四边形AMPN的面积最大,并求出最大值.
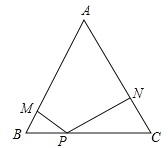
【答案】【(1)证明见解析;(2)当BP=1时,四边形AMPN的面积最大,最大值是![]() .
.
【解析】
试题(1)连接AP,过C作CD⊥AB于D,根据等边三角形的性质得到AB=AC,根据三角形的面积公式列方程即可得到结论;
(2)设BP=x,则CP=2﹣x,由△ABC是等边三角形,得到∠B=∠C=60°,解直角三角形得到BM=![]() x,PM=
x,PM=![]() x,CN=
x,CN=![]() (2﹣x),PN=
(2﹣x),PN=![]() (2﹣x),根据二次函数的性质即可得到结论.
(2﹣x),根据二次函数的性质即可得到结论.
试题解析:(1)连接AP,过C作CD⊥AB于D,
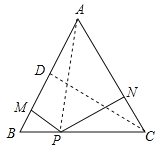
∵△ABC是等边三角形,∴AB=AC,∵S△ABC=S△ABP+S△ACP,∴![]() ABCD=
ABCD=![]() ABPM+
ABPM+![]() ACPN,∴PM+PN=CD,即不论点P在BC边的何处时都有PM+PN的长恰好等于三角形ABC一边上的高;
ACPN,∴PM+PN=CD,即不论点P在BC边的何处时都有PM+PN的长恰好等于三角形ABC一边上的高;
(2)设BP=x,则CP=2﹣x,∵△ABC是等边三角形,∴∠B=∠C=60°,∵PM⊥AB,PN⊥AC,∴BM=![]() x,PM=
x,PM=![]() x,CN=
x,CN=![]() (2﹣x),PN=
(2﹣x),PN=![]() (2﹣x),∴四边形AMPN的面积=
(2﹣x),∴四边形AMPN的面积=![]() ×(2﹣
×(2﹣![]() x)
x)![]() x+
x+![]() ×[2﹣
×[2﹣![]() (2﹣x)]
(2﹣x)] ![]() (2﹣x)=
(2﹣x)=![]() =
=![]() ,∴当BP=1时,四边形AMPN的面积最大,最大值是
,∴当BP=1时,四边形AMPN的面积最大,最大值是![]() .
.


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
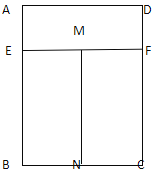
【题目】如图,矩形窗户边框ABCD由矩形AEFD,矩形BNME,矩形CFMN组成,其中AE:BE=1:3.已知制作一个窗户边框的材料的总长是6米,设BC=x(米),窗户边框ABCD的面积为S(米2)
(1)①用x的代数式表示AB;
②求x的取值范围.
(2)求当S达到最大时,AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴的交点分别为
轴的交点分别为![]() (1,0)、
(1,0)、![]() (3,0),与
(3,0),与![]() 轴的交点为
轴的交点为![]() .
.
(1)求抛物线的解析式和顶点坐标;
(2)点![]() (4,
(4,![]() )和
)和![]() (
(![]() ,
,![]() )为抛物线上的两点,当
)为抛物线上的两点,当![]() 时,写出
时,写出![]() 的取值范围;
的取值范围;
(3)在抛物线的对称轴上是否存在点![]() ,使
,使![]() 最大?若存在,请求出点
最大?若存在,请求出点![]() 的坐标;若不存在,请说明理由
的坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板![]() 与
与![]() (其中
(其中![]() ,
,![]() ,
,![]() )如图摆放,
)如图摆放,![]() 中
中![]() 所对的直角边与
所对的直角边与![]() 的斜边恰好重合。以
的斜边恰好重合。以![]() 为直径的圆经过点C,且与
为直径的圆经过点C,且与![]() 相交于点E,连接
相交于点E,连接![]() ,连接
,连接![]() 并延长交
并延长交![]() 于F.
于F.
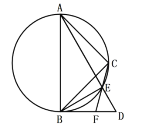
(1)求证:![]() 平分
平分![]() ;
;
(2)求![]() 与
与![]() 的面积的比值.
的面积的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共10只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)请估计:当![]() 很大时,摸到白球的频率将会接近 ;(保留二个有效数字)
很大时,摸到白球的频率将会接近 ;(保留二个有效数字)
(2)试估算口袋中黑、白两种颜色的球各有多少只?
(3)请画树状图或列表计算:从中一次摸两只球,这两只球颜色不同的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一组邻边相等的凸四边形叫做“和睦四边形”,寓意是全世界和平共处,睦邻友好,共同发展.如菱形,正方形等都是“和睦四边形”.
(1)如图1,BD平分∠ABC,AD∥BC,求证:四边形ABCD为“和睦四边形”;
(2)如图2,直线![]() 与x轴、y轴分别交于A、B两点,点P、Q分别是线段OA、AB上的动点.点P从点A出发,以每秒4个单位长度的速度向点O运动.点Q从点A出发,以每秒5个单位长度的速度向点B运动.P、Q两点同时出发,设运动时间为t秒.当四边形BOPQ为“和睦四边形”时,求t的值;
与x轴、y轴分别交于A、B两点,点P、Q分别是线段OA、AB上的动点.点P从点A出发,以每秒4个单位长度的速度向点O运动.点Q从点A出发,以每秒5个单位长度的速度向点B运动.P、Q两点同时出发,设运动时间为t秒.当四边形BOPQ为“和睦四边形”时,求t的值;
(3)如图3,抛物线![]() 与
与![]() 轴交于A、B两点(点A在点B的左侧),与y轴交于点
轴交于A、B两点(点A在点B的左侧),与y轴交于点![]() ,抛物线的顶点为点D.当四边形COBD为“和睦四边形”,且CD=OC.抛物线还满足:①
,抛物线的顶点为点D.当四边形COBD为“和睦四边形”,且CD=OC.抛物线还满足:①![]() ;②顶点D在以AB为直径的圆上. 点
;②顶点D在以AB为直径的圆上. 点![]() 是抛物线
是抛物线![]() 上任意一点,且
上任意一点,且![]() .若
.若![]() 恒成立,求m的最小值.
恒成立,求m的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=50 cm,EF=25 cm,测得边DF离地面的高度AC=1.6 m,CD=10 m,则树高AB等于( )

A. 4 m
B. 5 m
C. 6.6 m
D. 7.7 m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设D为锐角△ABC内一点,∠ADB=∠ACB+90°,过点B作BE⊥BD,BE=BD,连接EC.
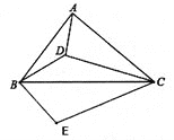
(1)求∠CAD+∠CBD的度数;
(2)若![]() ,
,
①求证:△ACD∽△BCE;
②求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com