
【题目】观察思考:如图, ![]() 、
、![]() 是直线
是直线![]() 上的两个定点,点
上的两个定点,点![]() 、
、![]() 在直线
在直线![]() 上运动(点
上运动(点![]() 在点
在点![]() 的左侧),
的左侧),![]() ,已知
,已知![]() ,
, ![]() 、
、![]() 间的距离为
间的距离为![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,把
,把![]() 沿
沿![]() 折叠得
折叠得![]() .
.
(![]() )当
)当![]() 、
、![]() 两点重合时,则
两点重合时,则![]() __________
__________ ![]() .
.
(![]() )当
)当![]() 、
、![]() 两点不重合时,
两点不重合时,
①连接![]() ,探究
,探究![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
②若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形,画出示意图并直接写出
为顶点的四边形是矩形,画出示意图并直接写出![]() 的长.
的长.


【答案】(1)4;
(2)①![]() ,理由见解析;②画图见解析,
,理由见解析;②画图见解析, ![]() 的长为
的长为![]() 或
或![]() 或
或![]() .
.
【解析】试题分析:(1)当A1、D两点重合时,可以证到四边形ACDB是菱形,从而得到AC=AB=4cm;
(2)①过点A1作A1E⊥BC,垂足为E,过点D作DF⊥BC,垂足为F,如图2,可以证到S△DBC=S△ABC=S△A1BC,从而得到DF=A1E,由A1E⊥BC,DF⊥BC可以证到A1E∥DF,从而得到四边形A1DFE是平行四边形,就可得到A1D∥BC;
②若以A1、C、B、D为顶点的四边形是矩形,则有三个位置,分别是图3①、图3②、图3③.对于图3①、图3②,过点C作CH⊥AB,垂足为H,运用相似三角形的性质建立方程就可求出AH,然后运用勾股定理就可求出AC的长;对于图3③,直接运用勾股定理就可求出AC的长.
试题解析:解:(1)当A1、D两点重合时,如图1①和图1②.
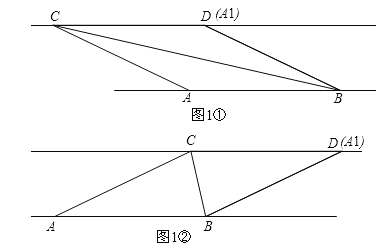
∵CD∥AB,CD=AB,∴四边形ACDB是平行四边形.
∵△ABC沿BC折叠得△A1BC,A1、D两点重合,∴AC=A1C=DC,∴平行四边形ACDB是菱形,∴AC=AB=4(cm).故答案为:4.
(2)当A1、D两点不重合时,①A1D∥BC.
证明:过点A1作A1E⊥BC,垂足为E,过点D作DF⊥BC,垂足为F,如图2.
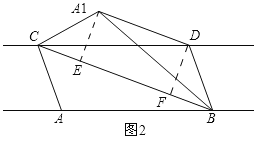
∵CD∥AB,CD=AB,∴四边形ACDB是平行四边形,∴S△ABC=S△DBC.
∵△ABC沿BC折叠得△A1BC,∴S△ABC=S△A1BC,∴S△DBC=S△A1BC,∴ ![]() BCDF=
BCDF=![]() BCA1E,∴DF=A1E.
BCA1E,∴DF=A1E.
∵A1E⊥BC,DF⊥BC,∴∠A1EB=∠DFB=90°,∴A1E∥DF,∴四边形A1DFE是平行四边形,∴A1D∥EF,∴A1D∥BC.
②Ⅰ.如图3①,过点C作CH⊥AB,垂足为H,此时AH<BH.
∵四边形A1DBC是矩形,∴∠A1CB=90°.
∵△ABC沿BC折叠得△A1BC,∴∠ACB=∠A1CB,∴∠ACB=90°.
∵CH⊥AB,∴∠AHC=∠CHB=90°,∴∠ACH=90°﹣∠HCB=∠CBH,∴△AHC∽△CHB,∴ ![]() ,∴CH2=AHBH.
,∴CH2=AHBH.
∵AB=4,CH=![]() ,∴3=AH(4﹣AH).
,∴3=AH(4﹣AH).
解得:AH=1或AH=3.
∵AH<BH,∴AH=1,∴AC2=CH2+AH2=3+1=4,∴AC=2.
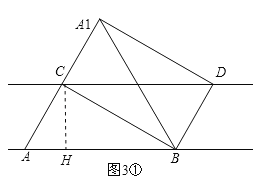
Ⅱ.如图3②,过点C作CH⊥AB,垂足为H,此时AH>BH.
同理可得:AH=3,∴AC2=CH2+AH2=3+9=12,∴AC=![]() .
.
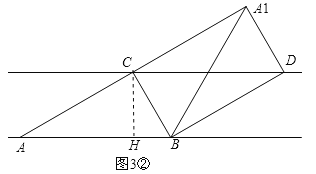
Ⅲ.如图3③,∵四边形A1DCB是矩形,∴∠A1BC=90°.∵△ABC沿BC折叠得△A1BC,∴∠ABC=∠A1BC,∴∠ABC=90°,∴AC2=BC2+AB2=3+16=19,∴AC=![]() .
.
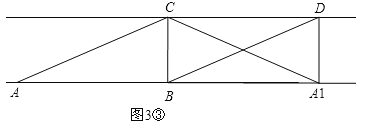
综上所述;当以A1、C、B、D为顶点的四边形是矩形时,AC的长为2或![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,DE是AC的垂直平分线.

(1)求证:△BCD是等腰三角形;
(2)△BCD的周长是a,BC=b,求△ACD的周长(用含a,b的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
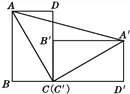
【题目】如图,将竖直放置的长方形砖块ABCD推倒至长方形A'B'C'D'的位置,长方形ABCD的长和宽分别为a,b,AC的长为c.
(1)你能用只含a,b的代数式表示S△ABC,S△C'A'D'和S直角梯形A'D'BA吗?能用只含c的代数式表示S△ACA'吗?
(2)利用(1)的结论,你能验证勾股定理吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块铁皮,拱形边缘呈抛物线状,MN=4,抛物线顶点处到边MN的距离是4,要在铁皮上截下一矩形ABCD,使矩形顶点B、C落在边MN上,A、D落在抛物线上.
(1)如图建立适当的坐标系,求抛物线解析式;
(2)设矩形ABCD的周长为L,点C的坐标为(m,0),求L与m的关系式(不要求写自变量取值范围).
(3)问这样截下去的矩形铁皮的周长能否等于9.5,若不等于9.5,请说明理由,若等于9.5,求出吗的值?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个盒子中装有质地、大小相同的小球,甲盒中有![]() 个白球、
个白球、![]() 个蓝球;乙盒中有
个蓝球;乙盒中有![]() 个白球、若干个蓝球,从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的
个白球、若干个蓝球,从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的![]() 倍.
倍.
(![]() )求乙盒中蓝球的个数.
)求乙盒中蓝球的个数.
(![]() )从甲、乙两盒中分别任意摸取一球,求这两球均为蓝球的概率.
)从甲、乙两盒中分别任意摸取一球,求这两球均为蓝球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
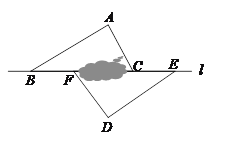
【题目】如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新农村社区改造中,有一部分楼盘要对外销售,某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120米2.
若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
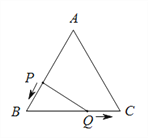
【题目】如图,已知△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1 cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s),则(1)BP![]() cm,BQ
cm,BQ![]() cm.(用含t的代数式表示)
cm.(用含t的代数式表示)
(2)当t为何值时,△PBQ是直角三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com