
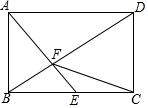
 如图,在矩形ABCD中,AB=$\sqrt{2}$,E是BC的中点,AE⊥BD于点F,则CF的长是$\sqrt{2}$.
如图,在矩形ABCD中,AB=$\sqrt{2}$,E是BC的中点,AE⊥BD于点F,则CF的长是$\sqrt{2}$. 分析 根据四边形ABCD是矩形,得到∠ABE=∠BAD=90°,根据余角的性质得到∠BAE=∠ADB,根据相似三角形的性质得到BE=1,求得BC=2,根据勾股定理得到AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{3}$,BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{6}$,根据三角形的面积公式得到BF=$\frac{AB•BE}{AE}$=$\frac{\sqrt{6}}{3}$,过F作FG⊥BC于G,根据相似三角形的性质得到CG=$\frac{4}{3}$,根据勾股定理即可得到结论.
解答  解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,
∴∠ABE=∠BAD=90°,
∵AE⊥BD,
∴∠AFB=90°,
∴∠BAF+∠ABD=∠ABD+∠ADB=90°,
∴∠BAE=∠ADB,
∴△ABE∽△ADB,
∴$\frac{AD}{AB}=\frac{AB}{BE}$,
∵E是BC的中点,
∴AD=2BE,
∴2BE2=AB2=2,
∴BE=1,
∴BC=2,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{3}$,BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{6}$,
∴BF=$\frac{AB•BE}{AE}$=$\frac{\sqrt{6}}{3}$,
过F作FG⊥BC于G,
∴FG∥CD,
∴△BFG∽△BDC,
∴$\frac{FG}{CD}$=$\frac{BF}{BD}$=$\frac{BG}{BC}$,
∴FG=$\frac{\sqrt{2}}{3}$,BG=$\frac{2}{3}$,
∴CG=$\frac{4}{3}$,
∴CF=$\sqrt{F{G}^{2}+C{G}^{2}}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查了矩形的性质,相似三角形的判定和性质,勾股定理,熟练掌握相似三角形的判定和性质是解题的关键.


科目:初中数学 来源: 题型:解答题
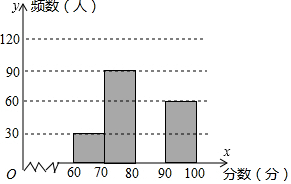 为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题:
为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题:| 组别 | 分数段(分) | 频数 | 频率 |
| A组 | 60≤x<70 | 30 | 0.1 |
| B组 | 70≤x<80 | 90 | n |
| C组 | 80≤x<90 | m | 0.4 |
| D组 | 90≤x<100 | 60 | 0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三角形的一个外角大于任何一个内角 | |
| B. | 任意多边形的外角和都是360° | |
| C. | 三角形任一边上的中线把原三角形分成两个面积相等的三角形 | |
| D. | 三角形的中线、角平分线、高线都是线段 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 个体是该校每一位学生 | |
| B. | 本校约有300名学生不知道自己母亲的生日 | |
| C. | 调查的方式是抽样调查 | |
| D. | 样本是随机调查的200名学生是否知道自己母亲的生日 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com