
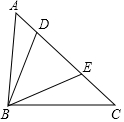
 如图,在△ABC中,点D,E是边AC的两点,且满足AE=AB,CB=CD,连接BD,BE,△BDE外接圆的面积为S1,△ABC内切圆的面积为S2,若DE=8,则S1-S2=16π.
如图,在△ABC中,点D,E是边AC的两点,且满足AE=AB,CB=CD,连接BD,BE,△BDE外接圆的面积为S1,△ABC内切圆的面积为S2,若DE=8,则S1-S2=16π. 分析 分别作∠BAC和∠ACB的角平分线AG、CF,相交于点H,首先说明H是△ABC的内心,H是△BDE的外心,作HI⊥DE于I,由垂径定理得:DI=EI.由DE=8可得,DI=EI=4连接DH,在Rt△DHI中,由勾股定理得DH2-HI2=DI2,由此即可解决问题.
解答 解:如图所示:分别作∠BAC和∠ACB的角平分线AG、CF,相交于点H,可知H是△ABC的 内心,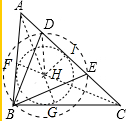
∵AB=AE、CB=CD,
∴AG垂直平分BE,CF垂直平分BD.
∴H点是△BDE的外心.
作HI⊥DE于I,由垂径定理得:DI=EI.
∵DE=8
∴DI=EI=4
连接DH,在Rt△DHI中,由勾股定理得
DH2-HI2=DI2
∴S1-S2=πDH2-πHI2=πDI2=π×42=16π,
故答案为16π.
点评 本题考查三角形的内切圆与内心,三角形的外接圆与外心等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
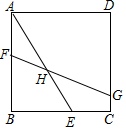 如图,在正方形ABCD中,AB=3,E为BC上一点,连接AE,H为AE的中点,过点H作直线FG交AB于F,交CD于G,若∠AHF=30°,AE=FG,则CG的长度为2-$\sqrt{3}$.
如图,在正方形ABCD中,AB=3,E为BC上一点,连接AE,H为AE的中点,过点H作直线FG交AB于F,交CD于G,若∠AHF=30°,AE=FG,则CG的长度为2-$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
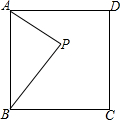 已知,如图,P是边长为5的正方形ABCD内一点,AP=3,BP=4,将△ABP绕点B旋转后,使P点落在直线BC上,点A落在点A′上,则线段A′C的长度为$\sqrt{10}$.
已知,如图,P是边长为5的正方形ABCD内一点,AP=3,BP=4,将△ABP绕点B旋转后,使P点落在直线BC上,点A落在点A′上,则线段A′C的长度为$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD内部画△ADP,使PA=PD,若∠APD=30°,点P在∠ABC的平分线上,则$\frac{AB}{BC}$的值是( )
如图,在矩形ABCD内部画△ADP,使PA=PD,若∠APD=30°,点P在∠ABC的平分线上,则$\frac{AB}{BC}$的值是( )| A. | $\frac{3+\sqrt{3}}{2}$ | B. | $\frac{2\sqrt{3}+3\sqrt{2}}{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | $\frac{5\sqrt{2}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,扇形和正方形ABCD,半径与AB重合,扇形的弧长和AB相等,已知AB=20,扇形沿着正方形翻滚到首次与起始位置相同,则点O经过的路径长为80+80π.
如图,扇形和正方形ABCD,半径与AB重合,扇形的弧长和AB相等,已知AB=20,扇形沿着正方形翻滚到首次与起始位置相同,则点O经过的路径长为80+80π.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 200名学生 | |
| B. | 3600名学生 | |
| C. | 每一名学生对“民族英雄范筑先”的知晓情况 | |
| D. | 所抽取的200名学生对“民族英雄范筑先”的知晓情况 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com