
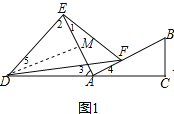
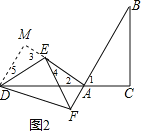
【题目】如图1所示,在Rt△ABC中,∠C=90°,点D是线段CA延长线上一点,且AD=AB.点F是线段AB上一点,连接DF,以DF为斜边作等腰Rt△DFE,连接EA,EA满足条件EA⊥AB.

(1)若∠AEF=20°,∠ADE=50°,AC=2,求AB的长度;
(2)求证:AE=AF+BC;
(3)如图2,点F是线段BA延长线上一点,探究AE、AF、BC之间的数量关系,并证明.
【答案】(1)![]() (2)证明见解析;(3)AE+AF=BC,证明见解析
(2)证明见解析;(3)AE+AF=BC,证明见解析
【解析】
试题分析:(1)在等腰直角三角形DEF中,∠DEF=90°,求得∠1=20°,根据余角的定义得到∠2=∠DEF﹣∠1=70°,根据三角形的内角和得到∠3=60°,∠4=30°根据三角函数的定义得到cos∠4=![]() ,于是得到结论;
,于是得到结论;
(2)如图1,过D作DM⊥AE于D,在△DEM中,由余角的定义得到∠2+∠5=90°,由于∠2+∠1=90°,推出∠1=∠5证得△DEM≌△EFA,根据全等三角形的性质得到AF=EM,根据三角形的内角和和余角的定义得到∠3=∠B,推出△DAM≌△ABC,根据全等三角形的性质得到BC=AM即可得到结论;
(3)如图2,过D作DM⊥AE交AE的延长线于M根据余角的定义和三角形的内角和得到∠2=∠B,证得△ADM≌△BAC,由全等三角形的性质得到BC=AM,由于EF=DE,∠DEF=90°,推出∠4=∠5,证得△MED≌△AFE,根据全等三角形的性质得到ME=AF,即可得到结论.
解:(1)在等腰直角三角形DEF中,∠DEF=90°,
∵∠1=20°,
∴∠2=∠DEF﹣∠1=70°,
∵∠EDA+∠2+∠3=180°,
∴∠3=60°,
∵EA⊥AB,
∴∠EAB=90°,
∵∠3+∠EAB+∠A=180°,
∴∠4=30°,
∵∠C=90°,
∴cos∠4=![]() ,
,
∴AB=![]() =
=![]() =
=![]() ;
;
(2)如图1,过D作DM⊥AE于D,在△DEM中,∠2+∠5=90°,
∵∠2+∠1=90°,
∴∠1=∠5,
∵DE=FE,
在△DEM与△EFA中,
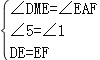 ,
,
∴△DEM≌△EFA,
∴AF=EM,
∵∠4+∠B=90°,
∵∠3+∠EAB+∠4=180°,
∴∠3+∠4=90°,
∴∠3=∠B,
在△DAM与△ABC中,
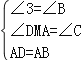 ,
,
∴△DAM≌△ABC,
∴BC=AM,
∴AE=EM+AM=AF+BC;
(3)如图2,过D作DM⊥AE交AE的延长线于M,
∵∠C=90°,
∴∠1+∠B=90°,
∵∠2+∠MAB+∠1=180°,∠MAB=90°,
∴∠2+∠1=90°,∠2=∠B,
在△ADM与△BAC中,
 ,
,
∴△ADM≌△BAC,
∴BC=AM,
∵EF=DE,∠DEF=90°,
∵∠3+∠DEF+∠4=180°,
∴∠3+∠4=90°,
∵∠3+∠5=90°,
∴∠4=∠5,
在△MED与△AFE中,
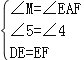 ,
,
∴△MED≌△AFE,
∴ME=AF,
∴AE+AF=AE+ME=AM=BC,
即AE+AF=BC.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:初中数学 来源: 题型:
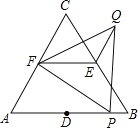
【题目】如图,△ABC和△FPQ均是等边三角形,点D、E、F分别是△ABC三边的中点,点P在AB边上,连接EF、QE.若AB=6,PB=1,则QE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南山植物园中现有A、B两个园区,已知A园区为长方形,长为(x+y)米,宽为(x﹣y)米;B园区为正方形,边长为(x+3y)米.
(1)请用代数式表示A、B两园区的面积之和并化简;
(2)现根据实际需要对A园区进行整改,长增加(11x﹣y)米,宽减少(x﹣2y)米,整改后A区的长比宽多350米,且整改后两园区的周长之和为980米.
①求x、y的值;
②若A园区全部种植C种花,B园区全部种植D种花,且C、D两种花投入的费用与吸引游客的收益如表:

求整改后A、B两园区旅游的净收益之和.(净收益=收益﹣投入)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真观察图形,解答下列问题:
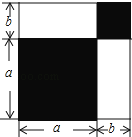
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①a+b的值;②a4﹣b4的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
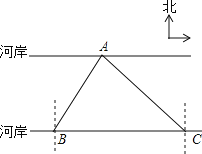
【题目】如图,要测量A点到河岸BC的距离,在B点测得A点在B点的北偏东30°方向上,在C点测得A点在C点的北偏西45°方向上,又测得BC=150m.求A点到河岸BC的距离.(结果保留整数)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com