
分析 根据直线的解析式求得A、B的坐标,进而求得∠ABO=30°,满足点C是y轴上一点,且△ABC是底角为30°的等腰三角形的C点只能在y轴的负半轴,故C的坐标与B点关于x轴对称,即可求得点C的坐标.
解答 解:∵一次函数y=-$\sqrt{3}$x+$\sqrt{3}$的图象分别与x轴、y轴交于点A、B,
∴A(1,0),点B(0,$\sqrt{3}$),
∵tan∠ABO=$\frac{OA}{OB}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠ABO=30°,
∵点C是y轴上一点,且△ABC是底角为30°的等腰三角形,
∴C(0,-$\sqrt{3}$).
点评 本题考查了一次函数图象上点的坐标特征,正切函数以及等腰三角形的判定,判定C的位置是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
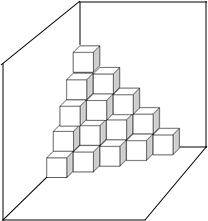 如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层.
如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将正六边形ABCDEF绕点B顺时针旋转后到达A′BC′D′E′F′的位置,所转过的度数是( )
如图,将正六边形ABCDEF绕点B顺时针旋转后到达A′BC′D′E′F′的位置,所转过的度数是( )| A. | 60° | B. | 72° | C. | 108° | D. | 120° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com