
| 物品重量(千克) | 支付费用(元) |
| 18 | 38 |
| 25 | 53 |
分析 (1)当x≤16时,只需付基础费30元+保险费a元,所以支付费用为(a+30)元;当x≥16时,需付费用为基础费30元+保险费a元+超重费,即[a+30+(x-16)b]元.
(2)①结合表格,根据当x≥16时,需付费用为基础费30元+保险费a元+超重费,列方程组求解;②能够托运,可以结合题意,分情况讨论,比如将物品拆成三件:两件均为16千克,另一件为18千克即可.
解答 解:(1)当x≤16时,支付的费用为:a+30;
当x≥16时,支付的费用为:a+30+(x-16)b.
故答案为:a+30,a+30+(x-16)b;
(2)①由题意得$\left\{\begin{array}{l}{a+30+(18-16)b=38}\\{a+30+(25-16)b=53}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{26}{7}}\\{b=\frac{15}{7}}\end{array}\right.$.
②托运方案是:
将物品拆成三件:两件均为16千克,另一种为18千克,
此时费用为:3×30+3×$\frac{26}{7}$+2×$\frac{15}{7}$=105.4(元)>105元.
∴用不超过105元的费用不能托运50千克物品.
点评 本题考查了二元一次方程组,一元一次不等式的应用,准确的找到等量关系并用方程组表示出来是解题的关键.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:解答题
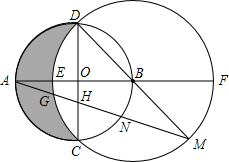 如图,已知⊙O的半径为R,直径AB⊥直径CD,以B为圆心,以BD为半径作⊙B交AB于E,交AB的延长线于F,连接DB并延长交⊙O于M,连接MA交⊙O于N,交CD于H,交⊙B于G.
如图,已知⊙O的半径为R,直径AB⊥直径CD,以B为圆心,以BD为半径作⊙B交AB于E,交AB的延长线于F,连接DB并延长交⊙O于M,连接MA交⊙O于N,交CD于H,交⊙B于G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com