
 ijһС����һ���ij��ٶȿ�ʼ��ǰ���������Ҿ��ȼ��٣�С��������ٶ�v����λ����/�룩��ʱ��x����λ���룩֮���ϵ�IJ����������һ��
ijһС����һ���ij��ٶȿ�ʼ��ǰ���������Ҿ��ȼ��٣�С��������ٶ�v����λ����/�룩��ʱ��x����λ���룩֮���ϵ�IJ����������һ��| ʱ��x���룩 | 0 | 1 | 2 | 2.5 | 3 | �� |
| �ٶ�v����/�룩 | 8 | 6 | 4 | 3 | 2 | �� |
| ʱ��x���룩 | 0 | 1 | 2 | 3 | �� |
| ����s���ף� | 0 | �� |
���� ��1���������$\overline{v}$��ֵ�������ֱ�ó�s��ֵ�����ɵó��𰸣�
��2�����ã�1��������������㼴�ɣ�
��3�����ô���ϵ����ȷ��������ϵʽ���ɣ�
��4������s=13.75���������루3���н���ʽ�����ó��𰸣�
��� �⣺��1��
��x=1ʱ��$\overline{v}$=$\frac{8+6}{2}$=7����s=7��1=7��
��x=2ʱ��$\overline{v}$=$\frac{8+4}{2}$=6����s=2��6=12��
��x=3ʱ��$\overline{v}$=$\frac{8+2}{2}$=5����s=3��5=15��
| ʱ��x���룩 | 0 | 1 | 2 | 3 | �� |
| ����s���ף� | 0 | 7 | 12 | 15 | �� |
 ��
������ ������Ҫ�����˶��κ�����Ӧ���Լ�����ϵ��������κ�������ʽ��֪ʶ����ȷ������������ǽ���ؼ���


 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABCΪ�ȱ������Σ��߳�Ϊ2��AB��x��ƽ�У�����C����Ϊ��2��$\sqrt{3}$+1�����涨�ѵȱߡ�ABC������x�ᷭ�ۣ�������ƽ��1����λ��Ϊһ�α任�����������������3�α任�ȱߡ�ABC�Ķ���A������Ϊ��4��-1�������������������2017�α任�ȱߡ�ABC�Ķ���A������Ϊ��2018��-1����
��ͼ����ABCΪ�ȱ������Σ��߳�Ϊ2��AB��x��ƽ�У�����C����Ϊ��2��$\sqrt{3}$+1�����涨�ѵȱߡ�ABC������x�ᷭ�ۣ�������ƽ��1����λ��Ϊһ�α任�����������������3�α任�ȱߡ�ABC�Ķ���A������Ϊ��4��-1�������������������2017�α任�ȱߡ�ABC�Ķ���A������Ϊ��2018��-1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�е��ı��ξ�Ϊ���Σ�����ͼ�Σ�д��һ����ȷ�ĵ�ʽ����m+n����a+b��=ma+mb+na+nb��
��ͼ�е��ı��ξ�Ϊ���Σ�����ͼ�Σ�д��һ����ȷ�ĵ�ʽ����m+n����a+b��=ma+mb+na+nb���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
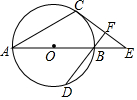 ��ͼ��AB�ǡ�O��ֱ����AC�ǡ�O���ң�E��AB�ӳ����ϵĵ㣬BF��EC��F����O��D����EBF=2��EAC��
��ͼ��AB�ǡ�O��ֱ����AC�ǡ�O���ң�E��AB�ӳ����ϵĵ㣬BF��EC��F����O��D����EBF=2��EAC���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com