
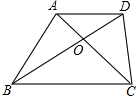
 如图,梯形ABCD中,AD∥BC,且AD:BC=1:3,对角线AC,BD交于点O,那么S△AOD:S△BOC:S△AOB=1:9:3.
如图,梯形ABCD中,AD∥BC,且AD:BC=1:3,对角线AC,BD交于点O,那么S△AOD:S△BOC:S△AOB=1:9:3. 分析 由梯形ABCD中,AD∥BC,可得△AOD∽△COB,然后由相似三角形的对应边成比例,可得OD:OB=1:3,根据等高三角形的面积比等于对应底的比,即可求得S△AOD:S△AOB的比值,又由相似三角形面积的比等于相似比的平方,求得S△AOD:S△BOC的比值,继而求得答案.
解答  解:∵梯形ABCD中,AD∥BC,
解:∵梯形ABCD中,AD∥BC,
∴△AOD∽△COB,
∵AD:BC=1:3,
∴OD:OB=AD:BC=1:3,
∴S△AOD:S△AOB=1:3,
∴S△AOD:S△BOC=1:9,
∴S△AOD:S△BOC:S△AOB=1:9:3.
故答案为1:9:3.
点评 此题考查了相似三角形的判定与性质以及三角形的面积.掌握等高三角形的面积比等于对应底的比,相似三角形面积的比等于相似比的平方的性质的应用是关键,注意数形结合思想的应用.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
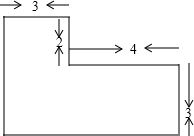 开放性试题:
开放性试题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
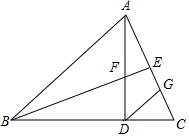 如图,在△ABC中,AB=BC,AD⊥BC于点D,点E为AC中点,连接BE交AD于点F,且BF=AC,过点D作DG∥AB,交AC于点G.
如图,在△ABC中,AB=BC,AD⊥BC于点D,点E为AC中点,连接BE交AD于点F,且BF=AC,过点D作DG∥AB,交AC于点G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
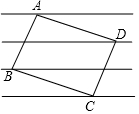 如图,矩形ABCD的四个顶点正好落在四条平行线上,并且从上到下每两条平行线间的距离都是1,如果AB:BC=3:4,那么AB的长是$\frac{\sqrt{73}}{4}$.
如图,矩形ABCD的四个顶点正好落在四条平行线上,并且从上到下每两条平行线间的距离都是1,如果AB:BC=3:4,那么AB的长是$\frac{\sqrt{73}}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com