
【题目】如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB的中点,则△EMN的周长是 . 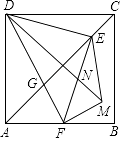
【答案】![]()
【解析】解:如图1,过E作PQ⊥DC,交DC于P,交AB于Q,连接BE, 
∵DC∥AB,
∴PQ⊥AB,
∵四边形ABCD是正方形,
∴∠ACD=45°,
∴△PEC是等腰直角三角形,
∴PE=PC,
设PC=x,则PE=x,PD=4﹣x,EQ=4﹣x,
∴PD=EQ,
∵∠DPE=∠EQF=90°,∠PED=∠EFQ,
∴△DPE≌△EQF,
∴DE=EF,
易证明△DEC≌△BEC,
∴DE=BE,
∴EF=BE,
∵EQ⊥FB,
∴FQ=BQ= ![]() BF,
BF,
∵AB=4,F是AB的中点,
∴BF=2,
∴FQ=BQ=PE=1,
∴CE= ![]() ,
,
Rt△DAF中,DF= ![]() =2
=2 ![]() ,
,
∵DE=EF,DE⊥EF,
∴△DEF是等腰直角三角形,
∴DE=EF= ![]() =
= ![]() ,
,
∴PD= ![]() =3,
=3,
如图2,∵DC∥AB,
∴△DGC∽△FGA,
∴ ![]() =
= ![]() =2,
=2,
∴CG=2AG,DG=2FG,
∴FG= ![]() ×
× ![]() =
= ![]() ,
,
∵AC= ![]() =4
=4 ![]() ,
,
∴CG= ![]() ×
× ![]() =
= ![]() ,
,
∴EG= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
连接GM、GN,交EF于H,
∵∠GFE=45°,
∴△GHF是等腰直角三角形,
∴GH=FH= ![]() =
= ![]() ,
,
∴EH=EF﹣FH= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
由折叠得:GM⊥EF,MH=GH= ![]() ,
,
∴∠EHM=∠DEF=90°,
∴DE∥HM,
∴△DEN∽△MNH,
∴ ![]() ,
,
∴ ![]() =
= ![]() =3,
=3,
∴EN=3NH,
∵EN+NH═EH= ![]() ,
,
∴EN= ![]() ,
,
∴NH=EH﹣EN= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
Rt△GNH中,GN= ![]() =
= ![]() =
= ![]() ,
,
由折叠得:MN=GN,EM=EG,
∴△EMN的周长=EN+MN+EM= ![]() +
+ ![]() +
+ ![]() =
= ![]() ;
;
故答案为: ![]() .
.
如图1,作辅助线,构建全等三角形,根据全等三角形对应边相等证明FQ=BQ=PE=1,△DEF是等腰直角三角形,利用勾理计算DE=EF= ![]() ,PD=
,PD= ![]() =3,如图2,由平行相似证明△DGC∽△FGA,列比例式可得FG和CG的长,从而得EG的长,根据△GHF是等腰直角三角形,得GH和FH的长,利用DE∥GM证明△DEN∽△MNH,则
=3,如图2,由平行相似证明△DGC∽△FGA,列比例式可得FG和CG的长,从而得EG的长,根据△GHF是等腰直角三角形,得GH和FH的长,利用DE∥GM证明△DEN∽△MNH,则 ![]() ,得EN=
,得EN= ![]() ,从而计算出△EMN各边的长,相加可得周长.
,从而计算出△EMN各边的长,相加可得周长.


科目:初中数学 来源: 题型:
【题目】某边防局接到情报,近海处有一可疑船只![]() 正向公海方向行驶,边防局迅速派出快艇
正向公海方向行驶,边防局迅速派出快艇![]() 追赶(如图1).图2中
追赶(如图1).图2中![]() 、
、![]() 分别表示两船相对于海岸的距离
分别表示两船相对于海岸的距离![]() (海里)与追赶时间
(海里)与追赶时间![]() (分)之间的关系.
(分)之间的关系.
(1)求![]() 、
、![]() 的函数解析式;
的函数解析式;
(2)当![]() 逃到离海岸12海里的公海时,
逃到离海岸12海里的公海时,![]() 将无法对其进行检查.照此速度,
将无法对其进行检查.照此速度,![]() 能否在
能否在![]() 逃入公海前将其拦截?若能,请求出此时
逃入公海前将其拦截?若能,请求出此时![]() 离海岸的距离;若不能,请说明理由.
离海岸的距离;若不能,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,ABCD是某公园的平面示意图,A、B、C、D分别是该公园的四个入口,两条主干道AC、BD交于点O,经测量AB=0.5km,AC=1.2km,BD=1km,请你帮助公园的管理人员解决以下问题:
(1)公园的面积为 km2;
(2)如图②,公园管理人员在参观了武汉东湖绿道后,为提升游客游览的体验感,准备修建三条绿道AN、MN、CM,其中点M在OB上,点N在OD上,且BM=ON(点M与点O、B不重合),并计划在△AON与△COM两块绿地所在区域种植郁金香,求种植郁金香区域的面积;
(3)若修建(2)中的绿道每千米费用为10万元,请你计算该公园修建这三条绿道投入资金的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)4992
(2)82018×(﹣0.125)2019
(3)3a2b(﹣![]() a4b2)+(a2b)3
a4b2)+(a2b)3
(4)(a+1)2﹣a(a﹣1)
(5)解二元一次方程组![]()
(6)先化简,再求值:(x+1)2﹣(x﹣1)(x+4),其中x=﹣2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分.而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的6位数密码就很有必要了.有一种用“因式分解法产生的密码,方便记忆,其原理是:将一个多项式分解因式,如多项式:x3+2x2﹣x﹣2因式分解的结果为(x﹣1)(x+1)(x+2),当x=18时,x﹣1=17,x+1=19,x+2=20,此时可以得到数字密码171920.
(1)根据上述方法,当x=21,y=7时,对于多项式x3﹣xy2分解因式后可以形成哪些数字密码?(写出两个)
(2)若多项式x3+(m﹣3n)x2﹣nx﹣21因式分解后,利用本题的方法,当x=27时可以得到其中一个密码为242834,求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
(进价、售价均保持不变,利润 = 销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
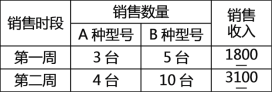
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化.如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=xcm,已知矩形的边BC=200m,边AB=am,a为大于200的常数,设四边形MNPQ的面积为sm2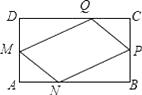
(1)求S关于x的函数关系式,并直接写出自变量x的取值范围.
(2)若a=400,求S的最大值,并求出此时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com