
【题目】已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.

(1)求证:BF=AC;
(2)求证:CE=![]() BF;
BF;
(3)CE与BG的大小关系如何?试证明你的结论.
【答案】(1)证明见解析;(2)证明见解析;(3)CE<BG.证明见解析.
【解析】
(1)证明△BDF≌△CDA,得到BF=AC;(2)由(1)问可知AC=BF,所以CE=AE=![]() BF;(3) BG=CG,CG在△EGC中,CE<CG.
BF;(3) BG=CG,CG在△EGC中,CE<CG.
解:(1)证明:因为CD⊥AB, ∠ABC=45°,
所以△BCD是等腰直角三角形.
所以BD=CD.
在Rt△DFB和Rt△DAC中,
因为∠DBF=90°-∠BFD, ∠DCA=90°-∠EFC,
又∠BFD=∠EFC,
所以∠DBF=∠DCA.
又因为∠BDF=∠CDA=90°,BD=CD,.
所以Rt△DFB≌Rt△DAC.
所以BF=AC.
(2)证明:在Rt△BEA和Rt△BEC中,
因为BE平分∠ABC,
所以∠ABE=∠CBE.
又因为BE=BE, ∠BEA=∠BEC=90°,
所以Rt△BEA≌Rt△BEC.
所以CE=AE=![]() AC.
AC.
又由(1),知BF=AC,
所以CE=![]() AC=
AC=![]() BF.
BF.
(3)CE<BG.证明:连接CG,
因为△BCD是等腰直角三角形,
所以BD=CD,
又H是BC边的中点,
所以DH垂直平分BC.
所以BG=CG,
在Rt△CEG中,
因为CG是斜边,CE是直角边,
所以CE<CG,即CE<BG.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
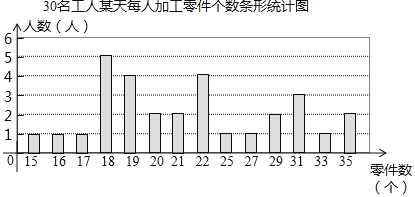
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
(1)①表中a的值为 ,中位数在第 组;
②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=5,AB的垂直平分线DE分别交AB,AC于E,D.
(1)若△BCD的周长为8,求BC的长;
(2)若BC=4,求△BCD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备印制一-批证书,现有两个印刷厂可供选择:
甲厂收费方式:收制版费1000元,每本印刷费0.5元;
乙厂收费方式:不超过2000本时,每本收印刷费1.5元;超过2000本时,超过的部分每本收印刷费0.25元,若该校印刷证书![]() 本.
本.
(1)若![]() 不超过2000时,甲厂的收费为 元,乙厂的收费为 元;
不超过2000时,甲厂的收费为 元,乙厂的收费为 元;
(2)若![]() 超过2000时,甲厂的收费为 元, 乙厂的收费为 元;
超过2000时,甲厂的收费为 元, 乙厂的收费为 元;
(3)当印制证书8000本时应该选择哪个印刷厂更节省费用?节省多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=![]() (m≠0,x>0)的图象交于第一象限内的A、B两点,过点A作AC⊥x轴于点C,AC=3,点B的坐标为(2,6)
(m≠0,x>0)的图象交于第一象限内的A、B两点,过点A作AC⊥x轴于点C,AC=3,点B的坐标为(2,6)

(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象,请直接写出y1<y2时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2019个格子中的数为__________.
3 |
|
|
| -1 | 2 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD于E,交AB于F,交⊙O于G。
(1)判断直线PA与⊙O的位置关系,并说明理由;
(2)求证:AG2=AF·AB;
(3)若⊙O的直径为10,AC=2![]() ,AB=4
,AB=4![]() ,求△AFG的面积.
,求△AFG的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com