
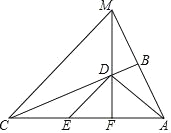
【题目】如图,∠ABC=90°,点D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB的延长线相交于点M,连接MC.
(1)MF与AC的位置关系是:______.
(2)求证:CF=MF.
(3)猜想:AD与MC的位置关系,并说明理由.
【答案】(1)MF⊥AC;(2)证明见解析;(3)AD⊥MC.
【解析】
(1)只要证明△ADE是等腰直角三角形,即可解决问题;
(2)根据等腰直角三角形的性质,得出DF⊥AE,DF=AF=EF,再证明△DFC≌△AFM,得出FC=FM;
(3)依据∠DFC=90°,DF=EF,∠FDE=∠FMC=45°,即可得到△DEF、△CFM是等腰直角三角形,进而证明DE∥MC,即可得出结论.
(1)∵AD⊥DE,AD=DE,
∴△ADE是等腰直角三角形,
∵AF=EF,
∴DF⊥AE,即MF⊥AC.
故答案为:MF⊥AC.
(2)∵AD⊥DE,且AD=DE,F是AE的中点,
∴DF⊥AE,DF=AF=EF,
∴∠AFM=90°,
∴∠FAM+∠AMF=90°,
∵∠ABC=90°,
∴∠FAM+∠DCF=90°,
∴∠DCF=∠AMF,
在△DFC和△AFM中,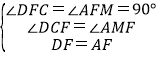 ,
,
∴△DFC≌△AFM(AAS),
∴FC=FM;
(3)AD⊥MC.
理由:由(2)得:∠DFC=90°,DF=EF,FM=FC,
∴△DEF、△CFM是等腰直角三角形,
∴∠FDE=∠FMC=45°,
∴DE∥MC,
∵AD⊥DE,
∴AD⊥MC.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,BC的垂直平分线分别交AB、BC于点D和点E,连接CD,AC=DC,∠B=25°,则∠ACD的度数是( )
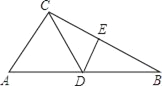
A. 50° B. 65° C. 80° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,已知点A(﹣1,0)、B(4,﹣1)、C(3,2).
(1)在所给的直角坐标系中画出△ABC;
(2)把△ABC向左平移3个单位,再向上平移2个单位得到△A′B′C′,画出△A′B′C′并写出点C′的坐标;
(3)求△A′B′C′的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点![]() 与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC的面积为84,BC=21,现将△ABC沿直线BC向右平移a(0<a<21)个单位到△DEF的位置.
(1)求BC边上的高;
(2)若AB=10,
①求线段DF的长;
②连结AE,当△ABE时等腰三角形时,求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
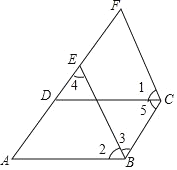
【题目】如图,已知![]() ,
,![]() ,
,![]() ,试说明:
,试说明:![]() .
.
完善下面的解答过程,并填写理由或数学式.
解:因为![]() (已知)
(已知)
所以![]() __________.
__________.
所以![]() (_________________).
(_________________).
因为![]() (已知)
(已知)
所以![]() _________.
_________.
所以![]() ,
,
所以![]() (_______________.)
(_______________.)
即:![]() .
.
因为![]() (已知)
(已知)
所以![]() (___________________.)
(___________________.)
即:![]() .
.
所以![]() (_____________________.)
(_____________________.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数p,q,我们用符号min{p,q}表示p,q两数中较小的数,如min{1,2}=1,因此,min{﹣ ![]() ,﹣
,﹣ ![]() }=;若min{(x﹣1)2 , x2}=1,则x= .
}=;若min{(x﹣1)2 , x2}=1,则x= .
查看答案和解析>>
科目:初中数学 来源: 题型:
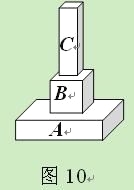
【题目】(11·大连)(本题10分)如图10,某容器由A、B、C三个长方体组成,其中
A、B、C的底面积分别为25cm2、10cm2、5cm2,C的容积是容器容积的![]() (容器各面的厚
(容器各面的厚
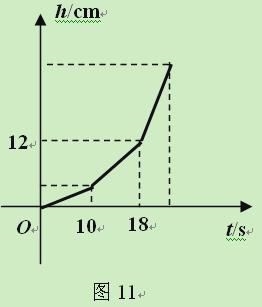
度忽略不计).现以速度v(单位:cm3/s)均匀地向容器注水,直至注满为止.图11是注水
全过程中容器的水面高度h(单位:cm)与注水时间t(单位:s)的函数图象.
⑴在注水过程中,注满A所用时间为______s,再注满B又用了_____s;
⑵求A的高度hA及注水的速度v;
⑶求注满容器所需时间及容器的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com