
【题目】若(a-2)0=1,则a的取范围是( )
A. a>2 B. a=2 C. a<2 D. a≠2
科目:初中数学 来源: 题型:
【题目】某校数学综合实践小组的同学以“绿色出行”为主题,把某小区的居民对共享单车的了解和使用情况进行了问卷调查.在这次调查中,发现有20人对于共享单车不了解,使用共享单车的居民每天骑行路程不超过8千米,并将调查结果制作成统计图,如下图所示:


(1)本次调查人数共 人,使用过共享单车的有 人;
(2)请将条形统计图补充完整;
(3)如果这个小区大约有3000名居民,请估算出每天的骑行路程在2~4千米的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过边长为3的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,且CQ=PA,连接PQ交AC于点D,则DE的长为( )
A.1
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
解:∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+(n2﹣8n+16)=0,
∴(m﹣n)2+(n﹣4)2=0,又∵(m﹣n)2≥0,(n﹣4)2≥0,
∴![]() , ∴n=4,m=4.
, ∴n=4,m=4.
请解答下面的问题:
(1)已知x2﹣2xy+2y2+6y+9=0,求xy﹣x2的值;
(2)已知△ABC的三边长a、b、c都是互不相等的正整数,且满足a2+b2﹣4a﹣18b+85=0,求△ABC的最大边c的值;
(3)已知a2+b2=12,ab+c2﹣16c+70=0,求a+b+c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“囧”(jiǒng)曾经是一个风靡网络的流行词,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y 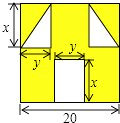
(1)用含有x、y的代数式表示右图中“囧”(阴影部分)的面积;
(2)当x=2,y=8时,求此时“囧”的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=α°,点P是∠AOB内任意一点,OP=6cm,点M和点N分别是射线OA和射线OB上的动点,若△PMN周长的最小值是6cm,则α的值是( )
A.15
B.30
C.45
D.60
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.
(1)如图1,若∠ABC=60°、∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.
①求证:CE=AG;
②若BF=2AF,连接CF,求∠CFE的度数;
(2)如图2,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,直接写出![]() 的结果
的结果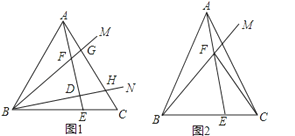
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com