
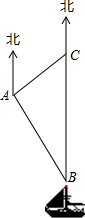
 南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+$\sqrt{3}$)海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+$\sqrt{3}$)海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离. 分析 作AD⊥BC,垂足为D,设CD=x,利用解直角三角形的知识,可得出AD,继而可得出BD,结合题意BC=CD+BD可得出方程,解出x的值后即可得出答案.
解答  解:如图,作AD⊥BC,垂足为D,
解:如图,作AD⊥BC,垂足为D,
由题意得,∠ACD=45°,∠ABD=30°.
设CD=x,在Rt△ACD中,可得AD=x,
在Rt△ABD中,可得BD=$\sqrt{3}$x,
又∵BC=20(1+$\sqrt{3}$),CD+BD=BC,
即x+$\sqrt{3}$x=20(1+$\sqrt{3}$),
解得:x=20,
∴AC=$\sqrt{2}$x=20$\sqrt{2}$(海里).
答:A、C之间的距离为20$\sqrt{2}$海里.
点评 此题考查了解直角三角形的应用,解答本题的关键是根据题意构造直角三角形,将实际问题转化为数学模型进行求解,难度一般.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
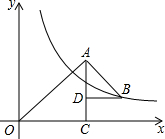 如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{6}{x}$在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC-S△BAD为( )
如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{6}{x}$在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC-S△BAD为( )| A. | 36 | B. | 12 | C. | 6 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
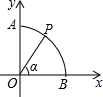 如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )| A. | (sinα,sinα) | B. | (cosα,cosα) | C. | (cosα,sinα) | D. | (sinα,cosα) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=-2 | B. | a=$\frac{1}{3}$ | C. | a=1 | D. | a=$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com