
【题目】观察猜想:
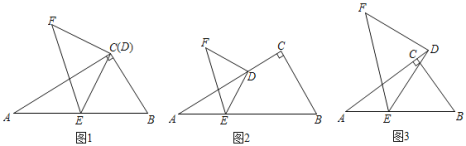
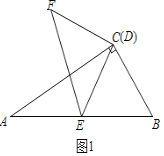
(1)如图1,在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D与点C重合,点E在斜边AB上,连接DE,且DE=AE,将线段DE绕点D顺时针旋转90°得到线段DF,连接EF,则![]() =______,sin∠ADE=________,
=______,sin∠ADE=________,
探究证明:
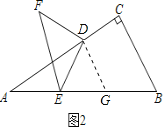
(2)在(1)中,如果将点D沿CA方向移动,使CD=![]() AC,其余条件不变,如图2,上述结论是否保持不变?若改变,请求出具体数值:若不变,请说明理由.
AC,其余条件不变,如图2,上述结论是否保持不变?若改变,请求出具体数值:若不变,请说明理由.
拓展延伸
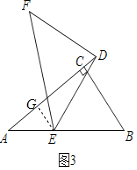
(3)如图3,在△ABC中,∠ACB=90°,∠CAB=a,点D在边AC的延长线上,E是AB上任意一点,连接DE.ED=nAE,将线段DE绕着点D顺时针旋转90°至点F,连接EF.求![]() 和sin∠ADE的值分别是多少?(请用含有n,a的式子表示)
和sin∠ADE的值分别是多少?(请用含有n,a的式子表示)
【答案】(1)![]() ;
;![]() ;(2)不变;(3)
;(2)不变;(3)![]() =
=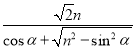 ;sin∠ADE=
;sin∠ADE=![]() .
.
【解析】
(1)由等腰三角形的性质和等边三角形的判定得到∠A=∠ACE=30°,△BEC是等边三角形,据此求得CE的长度,根据等腰直角三角形的性质来求EF的长度,易得答案;
(2)不变.理由:如图2,过点D作DG∥BC交AB于点G,构造直角三角形:△ADG,结合含30度角的直角三角形的性质和锐角三角函数的定义,结合方程求得答案;
(3)如图3,过点E作EG⊥AD于点G,构造直角三角形,根据锐角三角函数的定义列出方程并解答.
(1)如图1,∵在Rt△ABC中,∠ACB=90°,∠BAC=30°,
∴∠B=60°.
又CE=AE,
∴∠ACE=∠A=30°,
∴∠BCE=60°,
∴△BEC是等边三角形,
∴BE=CE.
∴AE=CE=BE.
∴AD=![]() AB=
AB=![]() CE.
CE.
又由旋转的性质知:FC=EC,∠FCE=90°,
∴EF=![]() CE,
CE,
∴![]() =
=![]() =
=![]() .
.
∵∠ADE=30°,
∴sin∠ADE=![]() .
.
故答案是:![]() ;
;![]() ;
;
(2)不变,理由:
如图2,过点D作DG∥BC交AB于点G,则△ADG是直角三角形.
∵∠DAG=30°,DE=AE,设DG=x,
∴∠AED=30°,AD=![]() x,∠DEG=∠DGE=60°.
x,∠DEG=∠DGE=60°.
∴DE=DF=x,sin∠ADE=![]() .
.
∵∠EDF=90°,
∴EF=![]() x.
x.
∴![]() =
=![]() =
=![]() .
.
∵∠ADE=30°,
∴sin∠ADE=![]() .
.
(3)过点E作EG⊥AD于点G,设AE=x,则DE=nx.
∵∠CAB=a,
∴AG=cosαx,EG=sinαx.
∴DG=![]() =
=![]() x.
x.
∴AD=cosαx+![]() x.
x.
∵∠EDF=90°,DE=DF,
∴EF=![]() DE=
DE=![]() nx.
nx.
∴![]() =
=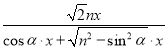 =
=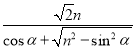 ,
,
sin∠ADE=![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
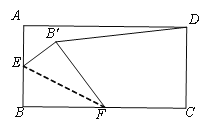
【题目】如图,矩形ABCD中,AD=4,AB=2.点E是AB的中点,点F是BC边上的任意一点(不与B、C重合),△EBF沿EF翻折,点B落在B'处,当DB'的长度最小时,BF的长度为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定,“中小学生每天在校体育锻炼时间不小于1小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:A组:时间小于0.5小时;B组:时间大于等于0.5小时且小于1小时;C组:时间大于等于1小时且小于1.5小时;D组:时间大于等于1.5小时.
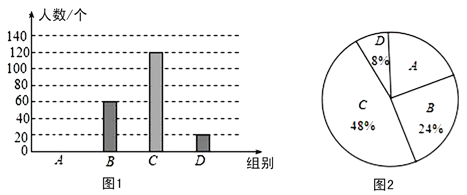
根据以上信息,回答下列问题:
(1)A组的人数是 人,并补全条形统计图;
(2)本次调查数据的中位数落在组 ;
(3)根据统计数据估计该地区25 000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等边三角形,点D在BC上,BD=2CD,点F是射线AC上的动点,点M是射线AD上的动点,∠AFM=∠DAB,FM的延长线与射线AB交于点E,设AM=x,△AME与△ABD重叠部分的面积为y,y与x的函数图象如图2所示(其中0<x≤m,m<x<n,x≥n时,函数的解析式不同).
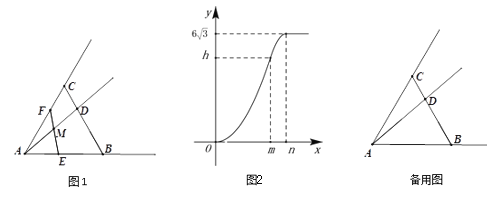
(1)填空:AB=_______;
(2)求出y与x的函数关系式,并求出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
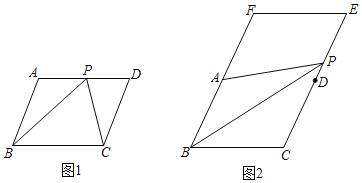
【题目】请分别在下列图中使用无刻度的直尺按要求画图.
(1)在图1中,点P是ABCD边AD上的中点,过点P画一条线段PM,使PM=![]() AB.
AB.
(2)在图2中,点A、D分别是BCEF边FB和EC上的中点,且点P是边EC上的动点,画出△PAB的一条中位线.
查看答案和解析>>
科目:初中数学 来源: 题型:
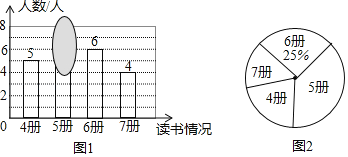
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.
(1)求条形图中被遮盖的数,并写出册数的中位数;
(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在达州市关工委组织的“五好小公民”主题教育活动中,我市某中学组织全校学生参加了“红旗队飘,引我成长”知识竞赛,赛后机抽取了部分参赛学生的成绩,从高分到低分将成绩分成![]() 五类,绘制成下面两个不完整的统计图:
五类,绘制成下面两个不完整的统计图:
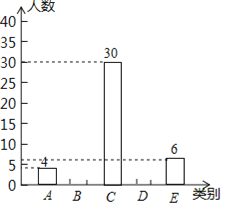
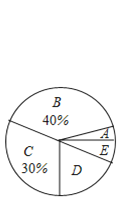
根据上面提供的信息解答下列问题:
(1)补全条形统计图;
(2)若该校共有学生4200人,求成绩为![]() 类的学生人数和
类的学生人数和![]() 类学生所对应的圆心角的度数;
类学生所对应的圆心角的度数;
(3)若![]() 类恰好是2名男生和2名女生,随机选择2名学生担任校园广播“孝心伴我行”节目主持人,请用列表法或画树状图法求恰好抽到1名男生和1名女生的概率.
类恰好是2名男生和2名女生,随机选择2名学生担任校园广播“孝心伴我行”节目主持人,请用列表法或画树状图法求恰好抽到1名男生和1名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com