
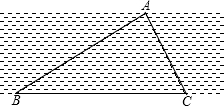
 如图,B、C是河岸边两点,A是对岸边上的一点,测得∠ABC=30°,∠ACB=45°,BC的长是30米,求河的宽度.(结果保留根号)
如图,B、C是河岸边两点,A是对岸边上的一点,测得∠ABC=30°,∠ACB=45°,BC的长是30米,求河的宽度.(结果保留根号)科目:初中数学 来源: 题型:
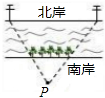 如图所示,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为
如图所示,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
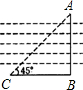 (2004•包头)如图,为了确定一条河的宽度AB,可以在点B一侧的岸边选择一点C,使得CB⊥AB,并量得CB=40米,测得∠ACB=45°,那么河的宽度AB是( )
(2004•包头)如图,为了确定一条河的宽度AB,可以在点B一侧的岸边选择一点C,使得CB⊥AB,并量得CB=40米,测得∠ACB=45°,那么河的宽度AB是( )查看答案和解析>>
科目:初中数学 来源: 题型:
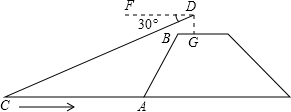
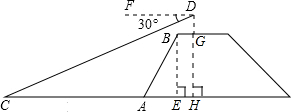 AE=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:
AE=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com