
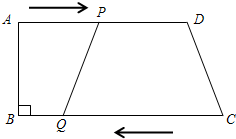
 如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.分析 (1)设经过ts时,四边形PQCD是平行四边形,根据DP=CQ,代入后求出即可;
(2)设经过ts时,四边形PQBA是矩形,根据AP=BQ,代入后求出即可;
(3)设经过t(s),四边形PQCD是等腰梯形,利用EP=2列出有关t的方程求解即可.
解答 解:(1)设经过x(s),四边形PQCD为平行四边形
即PD=CQ
所以24-x=3x,
解得:x=6.
(2)设经过y(s),四边形PQBA为矩形,
即AP=BQ,
所以y=26-3y,
解得:y=$\frac{13}{2}$.
(3)设经过t(s),四边形PQCD是等腰梯形.
过Q点作QE⊥AD,过D点作DF⊥BC,
∴∠QEP=∠DFC=90°
∵四边形PQCD是等腰梯形,
∴PQ=DC.
又∵AD∥BC,∠B=90°,
∴AB=QE=DF.
在Rt△EQP和Rt△FDC中,
$\left\{\begin{array}{l}{PQ=DC}\\{AB=DF}\end{array}\right.$,
∴Rt△EQP≌Rt△FDC(HL).
∴FC=EP=BC-AD=26-24=2.
又∵AE=BQ=26-3t,
∴EP=AP-AE=t-(26-3t)=2.
得:t=7.
∴经过7s,PQ=CD.
点评 此题主要考查平行四边形、矩形及等腰梯形的判定掌握情况,本题解题关键是找出等量关系即可得解.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{2}{5}}$ | B. | $\sqrt{x^2}$ | C. | $\sqrt{0.3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com