
【题目】已知A=x-2y,B=-x-4y+1.
(1)求2(A+B)-(A-B);(结果用含x,y的代数式表示)
(2)当![]() 与
与![]() 互为相反数时,求(1)中代数式的值.
互为相反数时,求(1)中代数式的值.
 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C. 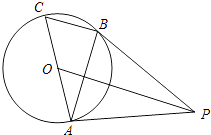
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为2 ![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q. 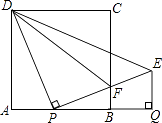
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有4张写着以下数字的卡片,请按要求抽出卡片,完成下列各题:
![]()
(1)从中取出2张卡片,使这2张卡片上数字之积最大,最大值是________.
(2)从中取出2张卡片,使这2张卡片上数字之差最小,最小值是________.
(3)从中取出4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使结果为24,请写出一种符合要求的运算式子________.(注:4个数字都必须用到且只能用一次.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y= ![]() 的图象过点A(1,2).
的图象过点A(1,2). 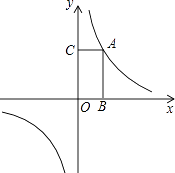
(1)求该函数的解析式;
(2)过点A分别向x轴和y轴作垂线,垂足为B和C,求四边形ABOC的面积;
(3)求证:过此函数图象上任意一点分别向x轴和y轴作垂线,这两条垂线与两坐标轴所围成矩形的面积为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个棱长为![]() 的正方体的每个面等分成
的正方体的每个面等分成![]() 个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去
个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去![]() 个小正方体),所得到的几何体的表面积是( )
个小正方体),所得到的几何体的表面积是( )

A. 78 B. 72 C. 54 D. 48
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com