
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).
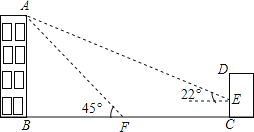
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2015次运动后,动点P的坐标是 . 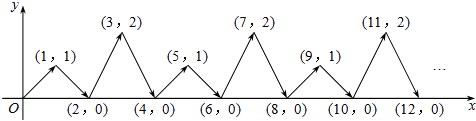
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90,AC=BC,OA=1,OC=4,抛物线y=![]() +bx+c经过A,B两点,抛物线的顶点为D.
+bx+c经过A,B两点,抛物线的顶点为D.
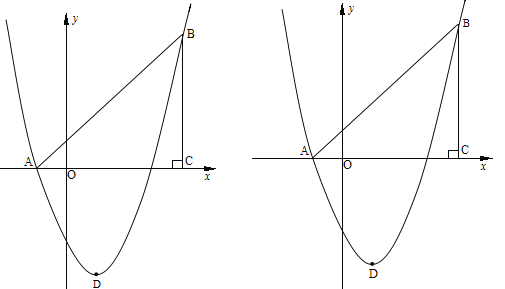
(1)、求b,c的值;
(2)、点E是直角三角形ABC斜边AB上一动点(点A、B除外),过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
(3)、在(2)的条件下:①求以点E、B、F、D为顶点的四边形的面积;②在抛物线上是否存在一点P,使△EFP是以EF为直角边的直角三角形? 若存在,求出所有点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.

(1)、求出将材料加热时,y与x的函数关系式;
(2)、求出停止加热进行操作时,y与x的函数关系式;
(3)、根据工艺要求,当材料的温度低于15℃时,须停止操作,那么操作时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+b﹣2|+ ![]() =0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D.
=0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D. 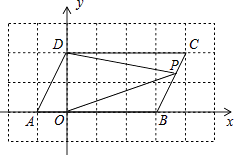
(1)请直接写出A、B、C、D四点的坐标并在坐标系中画出点A、B、C、D,连接AC,BD,CD.
(2)点E在坐标轴上,且S△BCE=S四边形ABDC , 求满足条件的点E的坐标.
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在线段BD上移动时(不与B,D重合)证明: ![]() 是个常数.
是个常数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com