
【题目】在直角坐标平面内,二次函数图像的顶点为A(1,﹣4),且过点B(3,0). 
(1)求该二次函数的解析式;
(2)将该二次函数图像向右平移几个单位,可使平移后所得图像经过坐标原点?并直接写出平移后所得图像与x轴的另一个交点的坐标.
【答案】
(1)解:∵二次函数图像的顶点为A(1,﹣4),
∴设二次函数解析式为y=a(x﹣1)2﹣4,
把点B(3,0)代入二次函数解析式,得:
0=4a﹣4,解得a=1,
∴二次函数解析式为y=(x﹣1)2﹣4,即y=x2﹣2x﹣3
(2)解:令y=0,得x2﹣2x﹣3=0,解方程,得x1=3,x2=﹣1.
∴二次函数图像与x轴的两个交点坐标分别为(3,0)和(﹣1,0),
∴二次函数图像上的点(﹣1,0)向右平移1个单位后经过坐标原点.
故平移后所得图像与x轴的另一个交点坐标为(4,0)
【解析】(1)有顶点就用顶点式来求二次函数的解析式;(2)由于是向右平移,可让二次函数的y的值为0,得到相应的两个x值,算出负值相对于原点的距离,而后让较大的值也加上距离即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知下面四个图形中,AB∥CD,探究四个图形中,∠APC与∠PAB,∠PCD的数量关系.
(1)图①中,∠APC与∠PAB,∠PCD的关系是__________________;
(2)图②中,∠APC与∠PAB,∠PCD的关系是__________________;
(3)请你在图③和图④中任选一个,说明∠APC与∠PAB,∠PCD的关系,并加以证明



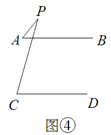
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过点A作AD⊥BP于点D,交直线BC于点Q.
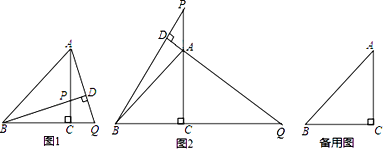
(1)如图1,当P在线段AC上时,求证:BP=AQ;
(2)如图2,当P在线段CA的延长线上时,(1)中的结论是否成立?________(填“成立”或“不成立”)
(3)在(2)的条件下,当∠DBA=________时,存在AQ=2BD,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第1次用39万元购进A、B两种商品,销售完后获得利润6万元,它们的进价和售价如下表:(总利润=单件利润×销售量)
商品 价格 | A | B |
进价(元/件) | 1200 | 1000 |
售价(元/件) | 1350 | 1200 |
(1)该商场第1次购进A、B两种商品各多少件?
(2)商场第2次以原价购进A、B两种商品,购进A商品的件数不变,而购进B商品的件数是第1次的2倍,A商品按原价销售,而B商品打折销售,若两种商品销售完毕,要使得第2次经营活动获得利润等于54000元,则B种商品是打几折销售的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元,售价为每件60元,每个月可卖出200件;如果每件商品的售价每上涨1元,则每个月少卖10件.设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)若每个月的利润不低于2160元,售价应在什么范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个自然数m,若将其数字重新排列可得一个新的自然数n,如果m=3n,我们称m是一个“希望数”.例如:3105=3×1035,71253=3×23751,371250=3×123750.
(1)请说明41不是希望数,并证明任意两位数都不可能是“希望数”.
(2)一个四位“希望数”M记为![]() ,已知
,已知![]() ,且c=2,请求出这个四位“希望数”.
,且c=2,请求出这个四位“希望数”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com