
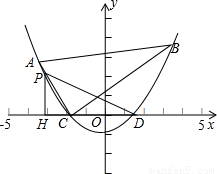
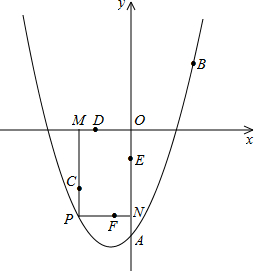
如图,已知二次函数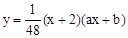 的图像过点A(-4,3),B(4,4).
的图像过点A(-4,3),B(4,4).
(1)求二次函数的解析式:
(2)求证:△ACB是直角三角形;
(3)若点P在第二象限,且是抛物线上的一动点,过点P作PH垂直x轴于点H,是否存在以P、H、D、为顶点的三角形与△ABC相似?若存在,求出点P的坐标;若不存在,请说明理由。
解:
(1)将A(-4,3),B(4,4)代人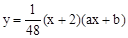 中,
中,
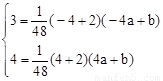 , 整理得:
, 整理得: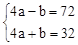 解得
解得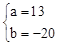
∴二次函数的解析式为: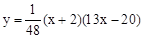 ,即:
,即: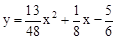 。
。
(2)由 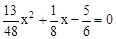 整理得
整理得
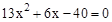 ,解得
,解得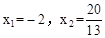 。
。
∴C (-2,0),D 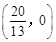 。
。
∴AC2=4+9 ,BC2=36+16,AC2+ BC2=13+52=65,AB2=64+1=65,
∴ AC2+ BC2=AB2 。∴△ACB是直角三角形。
(3)设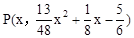 (x<0),则PH=
(x<0),则PH=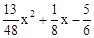 , HD=
, HD=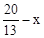 。
。
又∵AC=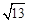 , BC=
, BC=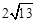 ,
,
①当△PHD∽△ACB时有: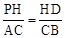 ,即:
,即: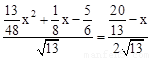 ,
,
整理得 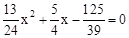 ,解得
,解得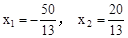 (舍去),此时,
(舍去),此时,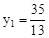 。
。
∴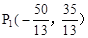 。
。
②当△DHP∽△ACB时有: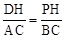 ,
即:
,
即: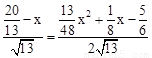 ,
,
整理  ,解得
,解得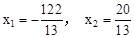 (舍去),此时,
(舍去),此时,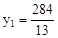 。
。
∴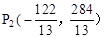 。
。
综上所述,满足条件的点有两个即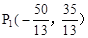 ,
,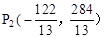 。
。
【解析】二次函数综合题,曲线上点的坐标与方程的关系,勾股定理和逆定理的应用,相似三角形的判定性质,坐标系中点的坐标的特征,抛物线与x轴的交点,解一元二次方程和二元一次方程组。
【分析】(1)求二次函数的解析式,也就是要求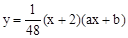 中a、b的值,只要把A(-4,3),B(4,4)代人即可。
中a、b的值,只要把A(-4,3),B(4,4)代人即可。
(2)求证△ACB是直角三角形,只要求出AC,BC,AB的长度,然后用勾股定理及其逆定理去考察。
(3)分两种情况进行讨论,①△DHP∽△BCA,②△PHD∽△BCA,然后分别利用相似三角形对应边成比例的性质求出点P的坐标。


科目:初中数学 来源: 题型:
 的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.
的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).
(2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).| 6 |
| 7 |
| 6 |
| 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•常德)如图,已知二次函数的图象过点A(0,-3),B(
(2013•常德)如图,已知二次函数的图象过点A(0,-3),B(| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知二次函数的图象与x轴交于A(2,0)、B(6,0)两点,与y轴交于点D(0,4).
如图,已知二次函数的图象与x轴交于A(2,0)、B(6,0)两点,与y轴交于点D(0,4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com