
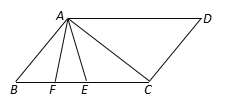
【题目】如图,AD∥BC,∠B=∠D=50°,点E、F在BC上,且满足∠CAD=∠CAE,AF平分∠BAE.

(1)∠CAF= °;
(2)若平行移动CD,那么∠ACB与∠AEB度数的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;
(3)在平行移动CD的过程中,是否存在某种情况,使∠AFB=∠ACD?若存在,求出∠ACD度数;若不存在,说明理由.
【答案】(1)65°;(2)不变,1:2;(3)存在,97.5°
【解析】
(1)根据角平分线的性质可得∠CAF=∠EAF+∠CAE=![]() ∠BAE+
∠BAE+![]() ∠DAE=
∠DAE=![]() ∠BAD,再根据平行线的性质得∠BAD =180-∠B,从而得出答案;
∠BAD,再根据平行线的性质得∠BAD =180-∠B,从而得出答案;
(2)根据平行线的性质得∠DAC=∠ACB,再由∠CAD=∠CAE,可知∠ACB=∠CAE,从而可得∠AEB =2∠ACB,即可得出答案;
(3)根据平行线的性质得∠AFB=∠DAF=∠DAC+∠CAF,∠ACD=∠CAB=∠BAF+∠CAF,再由平行线的性质可得∠BAD=130°,即可求出答案
解:(1)∵AF平分∠BAE,
∴∠BAF=∠EAF=![]() ∠BAE,
∠BAE,
∵∠CAD=∠CAE
∴∠CAD=∠CAE=![]() ∠DAE
∠DAE
∴∠CAF=∠EAF+∠CAE=![]() ∠BAE+
∠BAE+![]() ∠DAE=
∠DAE=![]() ∠BAD
∠BAD
∵AD∥BC,∠B=∠D=50°,
∴∠BAD=180-∠B=130°,
∴∠CAF=65°
(2)若平行移动CD,那么∠ACB与∠AEB度数的比值不发生变化.
∵AD∥BC,
∴∠DAC=∠ACB
∵∠CAD=∠CAE
∴∠ACB=∠CAE
∴∠AEB=∠CAE+∠ACB=2∠ACB
即∠ACB:∠AEB=1:2
所以,∠ACB与∠AEB度数的比值是:1:2;
(3)存在
∵AD∥BC,
∴∠B+∠BAD=180°,
∵∠B=∠D
∴∠D+∠BAD=180°
∴AB∥CD
∴∠AFB=∠DAF=∠DAC+∠CAF
∠ACD=∠CAB=∠BAF+∠CAF
∵∠AFB=∠ACD
∴∠DAC+∠CAF=∠BAF+∠CAF
∴∠DAC=∠BAF
∴∠DAC=∠BAF=∠CAE=∠EAF=![]() ∠BAD=
∠BAD=![]() ×130°=32.5°
×130°=32.5°
∴∠ACD= ∠CAB=∠BAF+∠CAF =3∠DAC=3×32.5°=97.5°


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
【题目】列方程解应用题:某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价-进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价-进价)

(1)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙种商品是按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有一点E,且EF=ED.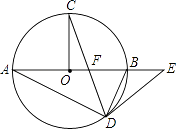
(1)求证:DE是⊙O的切线;
(2)若OF:OB=1:3,⊙O的半径R=3,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“镇康人民想致富,可惜差条二级路”这一啊数瑟小调流传镇康大街小巷.经有关部门批准,龙南二级路已于 2015 年初启动,已知两工程队共同参与某项筑路工程,甲队单独施工一个月完成总工程的![]() ,这时增加乙队,两队又共同工作了2个月,总工程全部完成.问:
,这时增加乙队,两队又共同工作了2个月,总工程全部完成.问:
(1)那个工程队的施工速度快?
(2)若甲、乙两队同时施工,需多少时间完成整项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天,小明从家里出发到图书馆去看书,再回到家.他离家的距离y(千米)与时间t(分钟)的关系如图所示.

根据图像回答下列问题:
(1)小明家离图书馆的距离是________千米;
(2)小明在图书馆看书的时间为________小时;
(3)小明去图书馆时的速度是________千米/小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.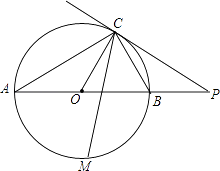
(1)求证:PC是⊙O的切线;
(2)求证:BC= ![]() AB;
AB;
(3)点M是 ![]() 的中点,CM交AB于点N,若AB=4,求MNMC的值.
的中点,CM交AB于点N,若AB=4,求MNMC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识解决下列问题.

(1)求△ABC的面积;
(2)判断△ABC是什么形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com