
1.观察发现
如题27(a)图,若点A,B在直线![]() 同侧,在直线
同侧,在直线![]() 上找一点P,使AP+BP的值最小. 做法如下:作点B关于直线
上找一点P,使AP+BP的值最小. 做法如下:作点B关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,与直线
,与直线![]() 的交点就是所求的点P
的交点就是所求的点P
再如题27(b)图,在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小.
如下:作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这
点就是所求的点P,故BP+PE的最小值为 .

2.实践运用
如题27(c)图,已知⊙O的直径CD为4,弧AD所对圆心角的度数为60°,点B是弧AD的中点,请你在直径CD上找一点P,使BP+AP的值最小,并求BP+AP的最小值.

3.拓展延伸
如题27(d)图,在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD.保留
作图痕迹,不必写出作法.

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源:2012届江西省南昌市九年级下学期第二次联考数学试卷(带解析) 题型:解答题
【小题1】观察发现
如题27(a)图,若点A,B在直线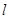 同侧,在直线
同侧,在直线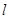 上找一点P,使AP+BP的值最小. 做法如下:作点B关于直线
上找一点P,使AP+BP的值最小. 做法如下:作点B关于直线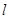 的对称点
的对称点 ,连接
,连接 ,与直线
,与直线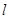 的交点就是所求的点P
的交点就是所求的点P
再如题27(b)图,在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小.
如下:作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这
点就是所求的点P,故BP+PE的最小值为 .
【小题2】实践运用
如题27(c)图,已知⊙O的直径CD为4,弧AD所对圆心角的度数为60°,点B是弧AD的中点,请你在直径CD上找一点P,使BP+AP的值最小,并求BP+AP的最小值.
【小题3】拓展延伸
如题27(d)图,在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD.保留
作图痕迹,不必写出作法.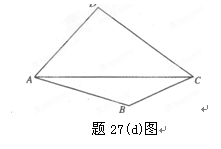
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江西省南昌市九年级下学期第二次联考数学试卷(解析版) 题型:解答题
1.观察发现
如题27(a)图,若点A,B在直线 同侧,在直线
同侧,在直线 上找一点P,使AP+BP的值最小. 做法如下:作点B关于直线
上找一点P,使AP+BP的值最小. 做法如下:作点B关于直线 的对称点
的对称点 ,连接
,连接 ,与直线
,与直线 的交点就是所求的点P
的交点就是所求的点P
再如题27(b)图,在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小.
如下:作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这
点就是所求的点P,故BP+PE的最小值为 .

2.实践运用
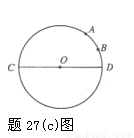
如题27(c)图,已知⊙O的直径CD为4,弧AD所对圆心角的度数为60°,点B是弧AD的中点,请你在直径CD上找一点P,使BP+AP的值最小,并求BP+AP的最小值.
3.拓展延伸
如题27(d)图,在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD.保留
作图痕迹,不必写出作法.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com