
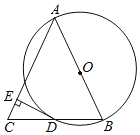
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC,垂足为E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线;
(3)若⊙O的半径为5,sinB=![]() ,求DE的长.
,求DE的长.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)连接AD,根据圆周角定理得到AD⊥BC,根据线段垂直平分线的性质证明;
(2)连接OD,根据三角形中位线定理得到OD∥AC,得到DE⊥OD,证明结论;
(3)解直角三角形求得AD,进而根据勾股定理求得BD、CD,据正弦的定义计算即可求得.
(1)证明:如图,连接AD,
∵AB是⊙O的直径,
∴AD⊥BC,又DC=BD,
∴AB=AC;
(2)证明:如图,连接OD,
∵AO=BO,CD=DB,
∴OD是△ABC的中位线,
∴OD∥AC,又DE⊥AC,
∴DE⊥OD,
∴DE为⊙O的切线;
(3)解:∵AB=AC,
∴∠B=∠C,
∵⊙O的半径为5,
∴AB=AC=10,
∵sinB=![]() =
=![]() ,
,
∴AD=8,
∴CD=BD=![]() =6,
=6,
∴sinB=sinC=![]() =
=![]() ,
,
∴DE=![]() .
.



科目:初中数学 来源: 题型:
【题目】尺规作图:如图,AD为⊙O的直径。

(1)求作:⊙O的内接正六边形ABCDEF.(要求:不写作法,保留作图痕迹);
(2)已知连接DF,⊙O的半径为4,求DF的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有![]() 、
、![]() 两个不透明的盒子,
两个不透明的盒子,![]() 盒中装有红色、黄色、蓝色卡片各1张,
盒中装有红色、黄色、蓝色卡片各1张,![]() 盒中装有红色、黄色卡片各1张,这些卡片除颜色外都相同.现分别从
盒中装有红色、黄色卡片各1张,这些卡片除颜色外都相同.现分别从![]() 、
、![]() 两个盒子中任意摸出一张卡片.
两个盒子中任意摸出一张卡片.
(1)从![]() 盒中摸出红色卡片的概率为______;
盒中摸出红色卡片的概率为______;
(2)用画树状图或列表的方法,求摸出的两张卡片中至少有一张红色卡片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为△ABD外接圆上的一动点(点C不在![]() 上,且不与点B,D重合),∠ACB=∠ABD=45°.
上,且不与点B,D重合),∠ACB=∠ABD=45°.
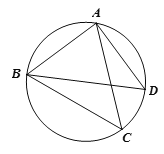
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:![]() AC=BC+CD;
AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究![]() ,
,![]() 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乐至县城有两座远近闻名的南北古塔,清朝道光11年至13年(公元1831--1833年)修建,南塔名为“文运塔”,高30米;北塔名为“凌云塔”.为了测量北塔的高度AB,身高为1.65米的小明在C处用测角仪CD,(如图所示)测得塔顶A的仰角为45°,此时小明在太阳光线下的影长为1.1米,测角仪的影长为1米.随后,他再向北塔方向前进14米到达H处,又测得北塔的顶端A的仰角为60°,求北塔AB的高度.(参考数据![]() ≈1.414,
≈1.414,![]() ≈1.732,结果保留整数)
≈1.732,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=60°,以O为圆心,以任意长为半径作弧,交OA,OB于点M,N,分别以点M,N为圆心,以大于![]() MN的长度为半径作弧,两弧在∠AOB内交于点P,以OP为边作∠POC=15°,则∠BOC的度数为( )
MN的长度为半径作弧,两弧在∠AOB内交于点P,以OP为边作∠POC=15°,则∠BOC的度数为( )
A.15°B.45°C.15°或30°D.15°或45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
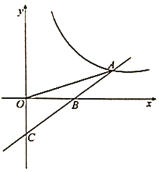
(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为x轴上一点,
为x轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
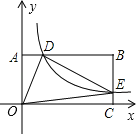
【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=![]() (x>0)的图象与AB相交于点D.与BC相交于点E,且BD=3,AD=6,△ODE的面积为15,若动点P在x轴上,则PD+PE的最小值是_____.
(x>0)的图象与AB相交于点D.与BC相交于点E,且BD=3,AD=6,△ODE的面积为15,若动点P在x轴上,则PD+PE的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a、b、c是常数,a<0)经过点A(-1,0)、B(3,0),顶点为C,则下列说法正确的个数是( )
①当-1<x<3时,ax2+bx+c>0;②当△ABC是直角三角形,则a=-![]() ;
;
③若m≤x≤m+3时,二次函数y=ax2+bx+c的最大值为am2+bm+c,则m≥3.
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com